レイノルズ数と相似則について流体解析の実例を示しながら説明します。
目次
レイノルズ数とは
レイノルズ数(Reynolds number)は慣性力と粘性力の比を表す無次元数で、流れの基本的な性質を表す重要な指標の一つです。
$U$:流速、$L$:代表長さ、$\nu$:動粘度、$\mu$:粘性係数、$\rho$:密度
当サイトの以下のページではレイノルズ数の値を計算することができます。
レイノルズの相似則
レイノルズ数に関する流体の性質としてレイノルズの相似則があります。これは長さのスケールの違う場合でもレイノルズ数が同じであれば、その流れ場は同じになるというものです。
例えば、実物の航空機の周りの流れとそれと相似な小さな模型の周りの流れは、レイノルズ数を合わせると同じ流れ場になるということです。そこで、取り扱いやすい模型を使って風洞実験などを行い、様々な測定データをとることができます。
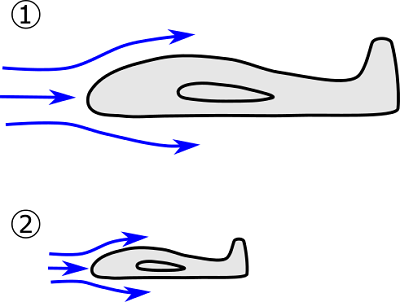
①実物、②模型の周りの流れ場
相似則の検証
では、相似則が実際に成り立つかを流体解析を使って確かめてみましょう。当サイトのオンライン流体解析ツールCATCFDzeroで流体計算を行います。
計算モデルはまず以下のような大きなモデルを考えます。高さ2mの凸型をした物体がx:15m、y:5mの領域中に置かれていて、左端から0.1m/sの流れが入ってくるとします。
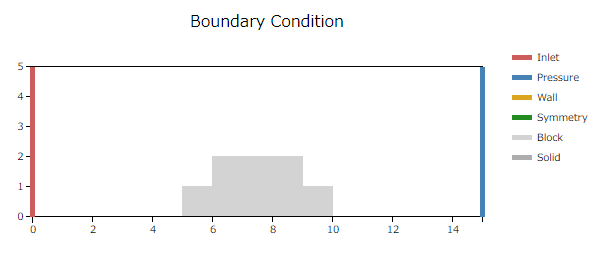
実物モデル
流体の物性は、密度1kg/m3、粘性係数0.001Pa sです。このときのレイノルズ数は $Re$ = 200となります。
この物体周りの流れ場は次のようになります。
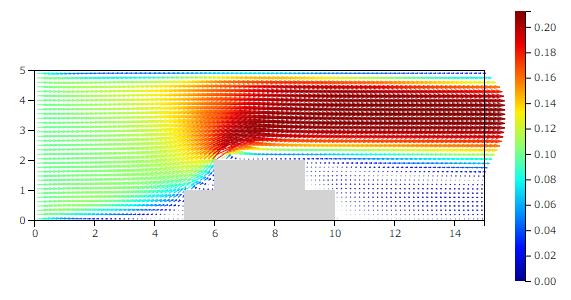
実物モデルの流れ場(Re=200)
次に、1/100スケールの模型を考えます。長さを全て1/100倍するので、物体の高さは0.02m=2cmです。物性値は同じ流体で計算してみます。
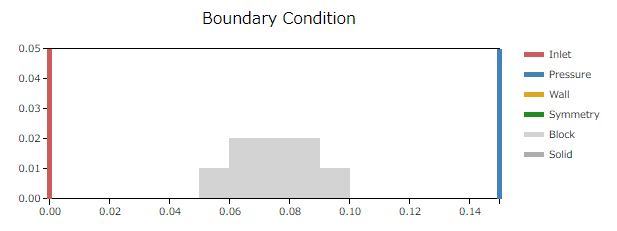
1/100モデル
もし、流入速度が同じ0.1m/sであるとすると、
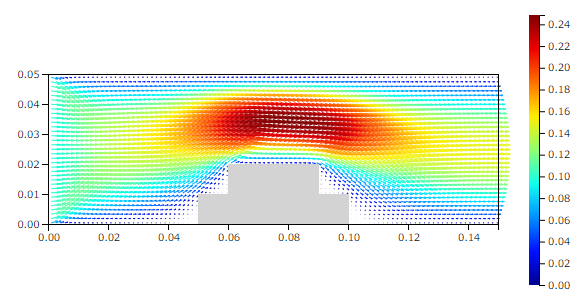
1/100モデルの流れ場(Re=2)
のような流れ場になります。ずいぶん流れ場が異なっていることがわかります。この条件でのレイノルズ数は $Re$ = 2です。
今度はレイノルズ数を合わせて$Re$ = 200とします。流入速度を変えて10m/sにすることでレイノルズ数を合わせることができます。このときの流れ場は、
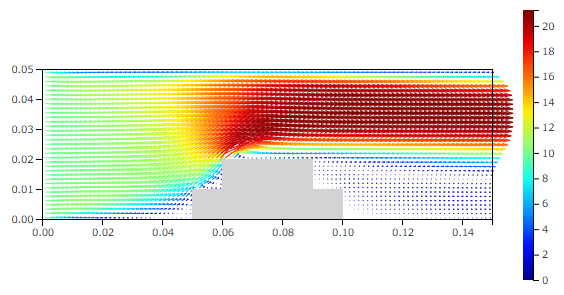
1/100モデルの流れ場(Re=200)
となります。流れ場の分布は元のスケールの流れ場と同じであることがわかります。(もちろん流入速度の大きさを変えているので、絶対値は異なりますが分布は同じです。)
このように、レイノルズ数を合わせることにより、長さスケールが違うモデルでも同じ分布の流れ場を得ることができます。
なお、(1)式からも明らかなように、レイノルズ数を合わせるやり方は流速を変えるだけではありません。流体の密度や粘度などの物性値を変えることができるのであれば、それらを調整して合わせることも可能です。
ナビエ=ストークス方程式とレイノルズ数
ここで、レイノルズ数により流れ場が決まるという相似則が、なぜ成り立つのかを数式の観点から説明しておきたいと思います。
非圧縮性流体のナビエ=ストークス方程式は次式で表せます(導出はこちら)。
ここで、代表長さ$L$、代表速度$U$で、各物理量を無次元化すると、
$${\bf v} = U {\bf v}^* \tag{3}$$
$${\bf x} = L {\bf x}^* \tag{4}$$
$$t = \frac{L}{U} t^* \tag{5}$$
$$ p = \rho U^2 p^* \tag{6}$$
と書けます。$*$付きは無次元化した量を表します。
これらを(2)式に代入し整理すると、無次元化したナビエ=ストークス方程式は、
$$\begin{split} \frac{D {\bf v}^*}{D t^*} &= -\nabla^* p^* + \frac{\mu}{\rho U L} \nabla^{*2} {\bf v}^* \\ &= -\nabla^* p^* + \frac{1}{Re} \nabla^{*2} {\bf v}^* \end{split} \tag{7}$$
となり、レイノルズ数$Re$のみがパラメータとして現れていることがわかります。
