オンライン熱解析ツールCATTHMで行なった定常熱伝導解析の結果と理論解を比較してみます。
目次
検証モデル
検証に使用するのは角柱の金属棒で1次元熱伝導で熱が伝わるモデルです。
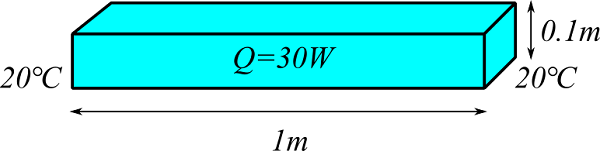
長さが1m、断面が0.1m×0.1mの金属棒(熱伝導率 20 W/(m K))で、両端を 20 ℃に固定し、他の面は断熱とします。この金属棒が一様に30Wで発熱した時の定常状態の温度分布を求めてみます。
解析モデル
解析モデルは、9個のノードからなる熱回路網モデルで、金属棒を7分割した中心位置と棒の両端に配置します。
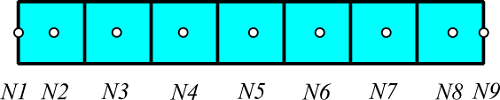
両端のN1、N9は 20 ℃に固定し、隣り合うノードは熱伝導による熱抵抗で接続します。N2~N8のノードには合計が30Wになるように均一に発熱量を与え、CATTHMで定常計算を行ないます。
理論解
このモデルは、次に示す1次元の定常熱伝導方程式で解くことができます。
$$\lambda \frac{\partial^2 T}{\partial x^2} + q = 0$$
ここで、$T$:温度、$x$:距離、$\lambda$:熱伝導率、$q$:単位体積あたりの発熱量。
この方程式は、今回の条件のもとで、解析的に解くことができ、以下のような理論解となります。
$$T = \frac{q}{2 \lambda} x (L-x)+T_0$$
ここで、$L$:棒の長さ、$T_0$:端の境界温度。
検証結果
温度分布のグラフを示します。
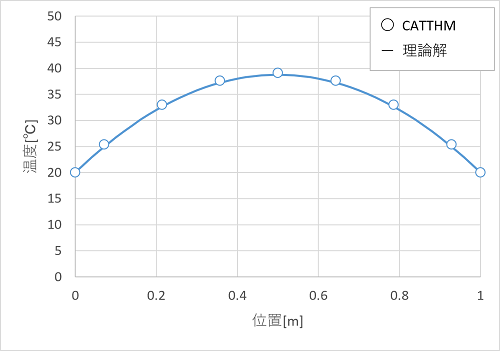
理論解を実線、CATTHMの結果を丸点で示しています。計算結果は、理論解とよく一致しています。
試しに、分割を粗くし、3分割しただけの熱回路モデルの結果を以下に示します。
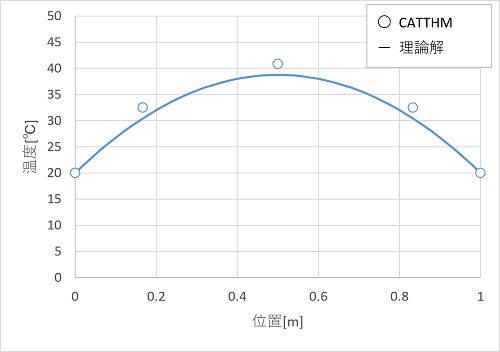
理論解よりは計算値の方が少し高いですが、近い結果は得られています。分割数が少なくても傾向をとらえるには十分使えるのではないかと思います。
熱回路網法の定式化
熱回路網法の定式化は、次式で表されます。
$$C_i \frac{d T_i}{d t} = \sum_j \frac{T_j - T_i}{R_{ij}}+Q_i$$
ここで、熱伝導による熱抵抗は、
$$R=\frac{\delta}{\lambda A}$$
$\delta$:ノード間距離、$A$:伝熱面積。
です。
詳細は以下のページを参照してください。
これは、フーリエの法則を使って、熱伝導方程式を導出する過程で出てくる式と同じ形になっています。以下のページの(6)式参照。
さらに、有限体積法で熱伝導方程式を離散化した式(以下のページの(4-4)~(4-13)式)とも同じ形式です。
要するに、熱回路網法の定式化は、ノード(コントロールボリューム)に出入りする熱流量の保存がきちんと考慮されていることになります。
したがって、ノードの数に依らず、全体の熱量のバランスはとれているわけです。もちろん、詳細な空間分布を捉えたい場合は、ノードの数を増やす必要がありますが、ざっくりした分布を計算するのであれば、少ないノード数でも熱量バランスのとれた結果を得ることができます。
差分法や有限体積法で細かいメッシュで計算すると空間分布の精度は高くなりますが、計算時間などのコストも高くなってしまいます。一方、熱回路網法はノード数を減らして計算時間を短くすることができ、計算コストの観点からも有益な手法であると言えます。
