流線・流跡線・流脈線

流体の流れを視覚的に表すのに流体の道筋を線で表示することがあります。今回はその表示方法である流線・流跡線・流脈線について解説します。

流線

流れをある瞬間で見たときに、流れを表す速度ベクトルが曲線の接線となるようなその曲線を流線といいます。

流線

流線の方程式は流線の微小要素を$(dx, dy, dz)$、速度ベクトルを$(u_x, u_y, u_z)$とすると、

$$\frac{dx}{u_x} = \frac{dy}{u_y} =\frac{dz}{u_z}$$

と表せます。

実際の水の流れで流線を可視化する場合、水面に粉状の微粒子を一様にまき、短時間の露出で写真をとります。すると、粒子が短い線となって写ります。この線を連ねたものが流線です。

一つの流体粒子を考えたとき、その粒子が時間経過とともに移動した軌跡を流跡線と言います。

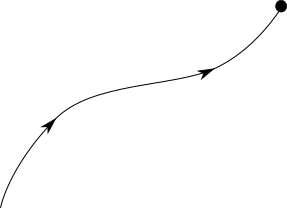
流跡線

流跡線の式は微小時間$dt$の間に微小要素だけ移動することを考えると、

$$\frac{dx}{u_x} = \frac{dy}{u_y} =\frac{dz}{u_z} = dt$$

となります。

流跡線は水面のある一点に落とした粉末粒子を長時間の露出で撮影します。そうすると、粒子の軌跡を撮ることができます。これが流跡線です。

空間のある点$x_0$を次々に通過した流体粒子が、ある時刻に到達した点をつないだ線を流脈線と呼びます。

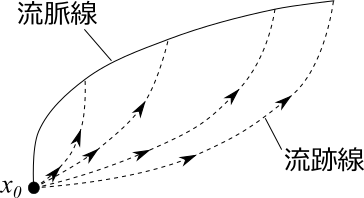
$x_0$を通る流跡線のある時刻における位置をつないだ線とも言えます。

流脈線は水面のある一点に継続して粒子を落とし、いくらか時間が経過した後に写真をとります。このときの粒子を連ねて見ると流脈線になっています。

一般的に流れ場に非定常性があり時々刻々変化する流れでは、流線・流跡線・流脈線はそれぞれ異なった線として描かれます。

しかし、時間的に変化しない定常流では、流線・流跡線・流脈線は全て一致します。

では、CATCFDzeroで流線を描いてみましょう。CATCFDzeroは定常計算のみできるので、流線は流跡線、流脈線に一致しています。

下端の左から流入し、右端の上部に流出する流れを計算します。

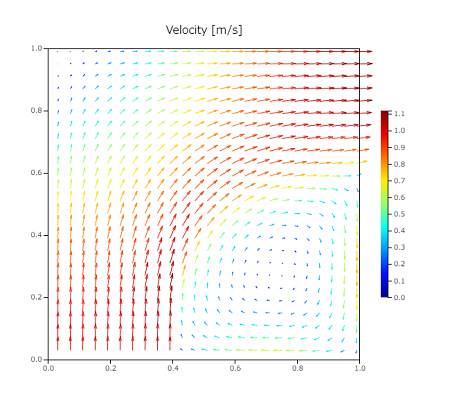
速度ベクトル

この流線は次のようになっています。速度コンターに白色で流線を表示しています。

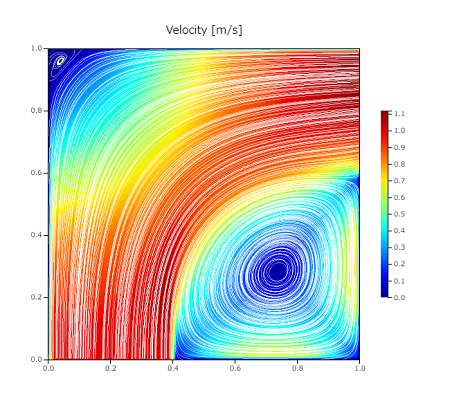
流入部から出口へ向かって流線が伸びています。また、右下角には円状の閉じた流線があります。これはここで渦が発生しており閉じた流れになっていることを表しています。

このように流線を見ると流れ場の様子がよくわかります。