目次
はじめに
前回のコラムでベルヌーイの定理の誤解について検証してみました。
今回はコアンダ効果について流体解析を行い、流れ場の詳細を確認してみたいと思います。
コアンダ効果とは
コアンダ効果も、身近な科学実験などでよく出てきます。ベルヌーイの定理と同じくらい流体現象をコアンダ効果で説明したものを見かけます。
コアンダ効果は「種々の条件下で流れが壁に付着する現象」の一般的な名称です[1]。
例えば噴流のそばに壁がある場合の流体解析を行ってみます。解析は当サイトのCATCFDzeroを使います。
※CATCFDzeroは非圧縮性、定常、2次元の流体コードのため、圧縮性や非定常性、3次元性が顕著な場合は、分布や絶対値が実際と異なる場合があることにご注意ください。
下図の結果は、10mm径のパイプから20m/sで噴出される条件です。
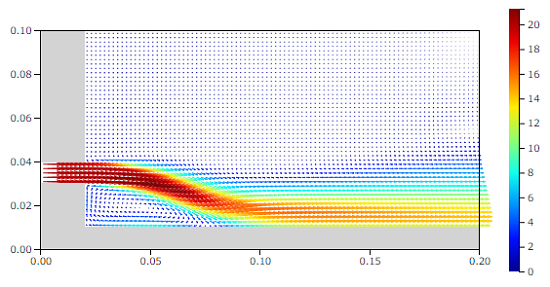
速度ベクトル[m/s]
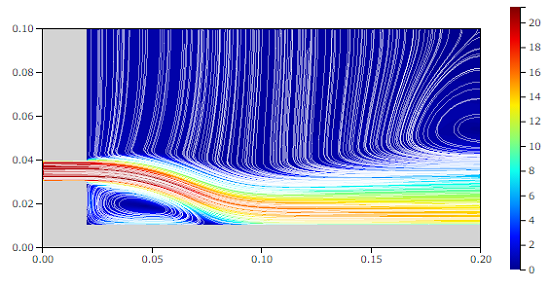
流線と速度[m/s]
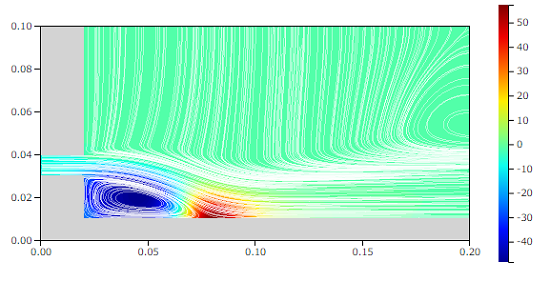
流線と圧力[Pa]
吹き出された噴流の下に壁がありますが、噴流は壁に付着し壁面に沿って流れていくようすが分かります。
この現象のメカニズムは、前回ベルヌーイの定理の検証の時に見た噴流の性質を思い出すと分かります。大気中に噴出された噴流は、粘性によってまわりの空気を取り込みながら(エントレインメント)、下流に輸送される流体の量を増加させていきます。
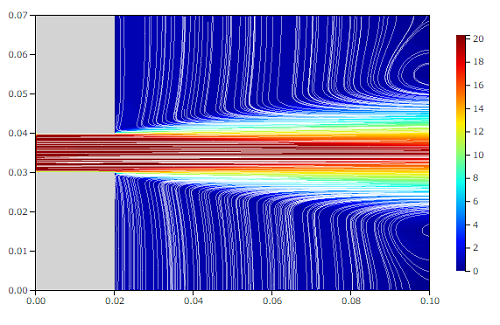
噴流の流速[m/s]と流線
まわりに壁が無い自由噴流の場合は、空気の取り込みがスムーズに行われますが、壁があると空気をうまく引き込めません。無理に引き込むと負圧になるため、壁を吸い寄せるか(*)、壁が動かない場合は噴流自身が壁に向かって引き寄せられることになります。
※前回のコラムのコの字の紙の実験を参照。
なおより一般的には、噴流ではない一様流でも「凸型の曲面上を壁面に沿って流れる場合はコアンダ効果による」という説明を見かけます。ただし、文献[1]では「すべての場合に同じ力学的なメカニズムが働いているかどうかは疑問である」と述べられています。確かにコアンダ効果を統一的に表す理論式のようなものが無いので、どのようなメカニズムによる現象かは名称にとらわれず、個別にみて議論した方がよさそうです。
円筒を吹いて倒す実験
ここでは、噴流が曲面に沿って流れるコアンダ効果の実験をひとつ取り上げてみます。
空き缶やトイレットペーパーの芯、ペットボトルなど軽い円筒形の物体(できるだけ軽い方がいいです)を机の上に置きます。そして、ストローで中心より端の方をめがけて吹いてみます。
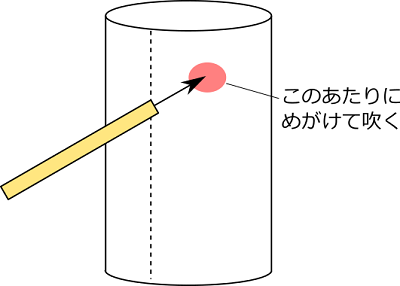
実際にやってみると、吹いている側の前方(この例だと右前方)に倒れます。
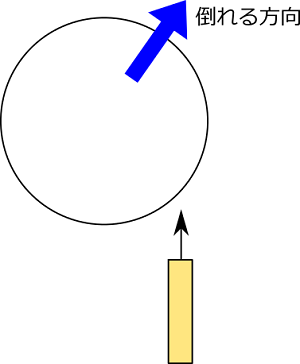
※割り箸などの上に円筒を置いて倒しやすくすると、右側に倒れます。
このとき、どの様な流れになっているかを流体解析で検証してみます。
図のように、Φ60mmの円筒の中心から右に寄った位置に向かって10mm径のパイプから20m/sで空気を噴出させます。
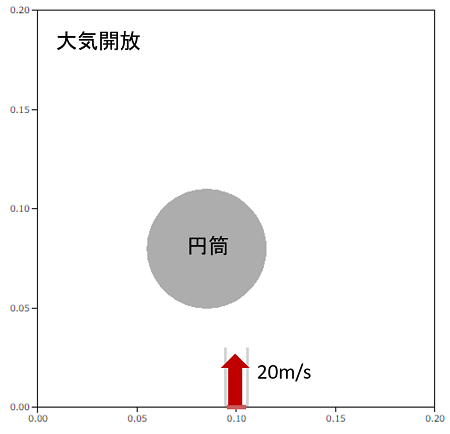
この条件で、流れ場は次のような結果になりました。
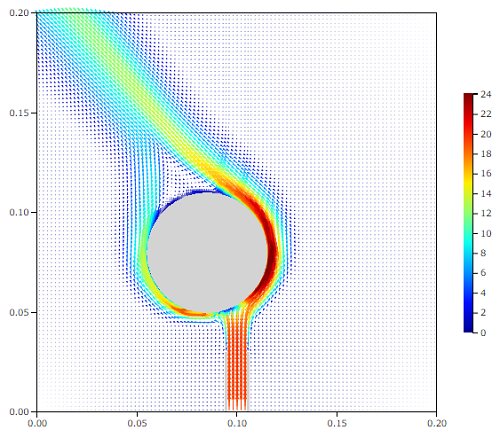
速度ベクトル[m/s]
パイプから出た噴流は円筒の右側前面に衝突し左右に分かれます。形状から考えて明らかに、右側に分かれる量が多くなっています。右側に分かれた流れは、円筒の壁面に沿って流れていきます。その時、円筒表面に近いところでは流速が速くなっていることがわかります。壁面に沿った流れは円筒を回り込み、円筒の後部ではく離し、画面の左側に吐出しています。
噴流が円筒に衝突する点から左側に分かれた流れも、同様に一部で加速し、円筒を回り込んでいます。そして、円筒後部で剥がれていき、最後右側から回り込んだ流れと合流して左側に吐出しています。
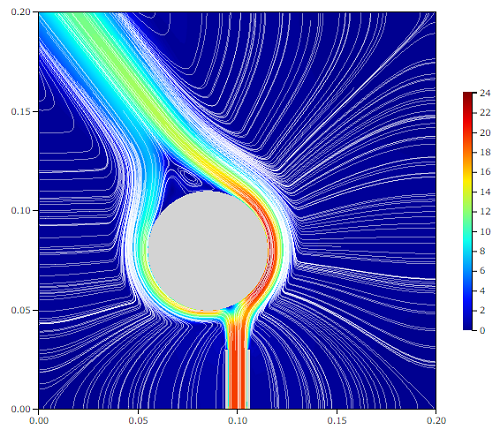
流線と速度[m/s]
流線を見ると噴流が壁面に沿って流れる道筋と、まわりからエントレインメントされる空気が合流していく様子がよくわかります。
このときの圧力は下図のようになっています。
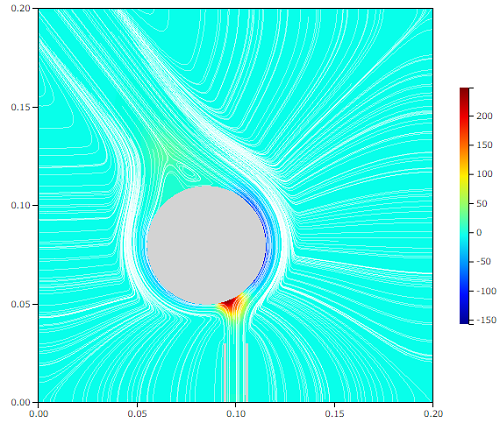
流線と圧力[Pa]
まず、パイプから噴出された噴流が円筒と衝突する位置では、圧力が高くなっています。ちょうど衝突点はよどみ点となり噴流の動圧が静圧に変換され、圧力が高くなります。よどみ点ですべての動圧が静圧になるとすると、
$$p_s = \frac{1}{2} \rho u^2 \tag{1}$$
ここで、$p_s$:よどみ圧、$\rho$:密度、$u$:流速
なので、流速20m/s、密度1.205kg/m3から換算される圧力は、241Paとなり計算結果とほぼ一致しています。
次に円筒の右側を回る流れの箇所では、円筒の表面に沿って圧力の低い領域ができています。このとき、流体は円筒の表面に沿って円運動をしていることになります。流線は円に沿って曲がっていることがわかります。この場合、流体は遠心力により内側より外側が圧力が高くなります。今回の場合、外側は大気圧なので、内側は大気圧より小さくなります。このように、流線の曲率により壁面に垂直な方向の圧力勾配が生じる現象は、流線曲率の定理と呼ばれています。
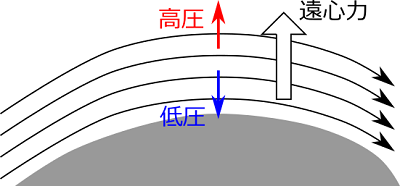
流線曲率の定理では、非粘性で外力が無視できる定常流れの場合、圧力勾配は
$$\frac{\partial p}{\partial r} = \rho \frac{u^2}{r} \tag{2}$$
ここで、$p$:圧力、$r$:流線の曲率半径
と表されます。
今回の結果から、円筒の右側に沿う噴流の流速は24m/s程度で、曲率半径30mmとすると、(2)式より圧力勾配は約23000Pa/mとなり、5mm程度の層だと115Pa程度の圧力低下となり、おおむね結果に合っています(実際には分布があったり、粘性の影響があるためあくまで概算です)。
また、円筒の左側を回る流れも同様に圧力低下が見られますが、流速が遅いため圧力低下は右側に比べて小さくなっています。
円筒にかかる力はこれらの圧力の合力となります(厳密には壁面せん断応力もかかりますが、今回の条件では壁面せん断応力は小さいのでほぼ圧力によって力が決まります)。この計算では、画面の右方向に2.31N、上方向に1.90Nの力が加わっており、円筒は右上方向に倒れることがわかります(力の値は単位長さあたり)。

なお、コアンダ効果では作用反作用で力を説明する場合があります。パイプから前方に噴出された流れは、最終的に円筒により左方向に曲げられ、吐出されています。流れが左に曲げられるということは、その反作用として円筒は右方向への力が加わることになります。
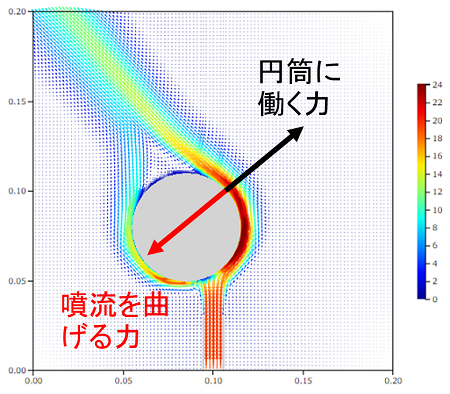
なお、実際に流れの方向を確かめるには、糸や細く切ったティッシュペーパーをかざしてみるとすぐ分かります。上図で円筒を回り込んだ流れが左側に吐出しているあたりにあてると、流れがある様子がよくわかると思います。
まとめ
コアンダ効果と呼ばれる現象について流体解析を行ってみました。流れや圧力分布を実際に見ると、言葉や概念図で説明されるより、物体に働く力の様子がよくわかります。
コアンダ効果は、空調機器や航空機、自動車などでも応用され実用になっている例があるのでぜひ探してみてください。