非定常熱伝導解析の検証

オンライン熱解析ツールCATTHMで行なった非定常熱伝導解析の結果と理論解を比較してみます。

検証モデル

検証に使用するのは角柱の金属棒で１次元熱伝導で熱が伝わるモデルです。

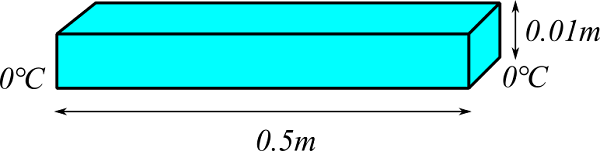
長さが0.5m、断面が0.01m×0.01mの金属棒（密度 7800 kg/m3、比熱 460 J/(kg K)、熱伝導率 27 W/(m K)）で、両端を 0 ℃に固定し、他の面は断熱とします。

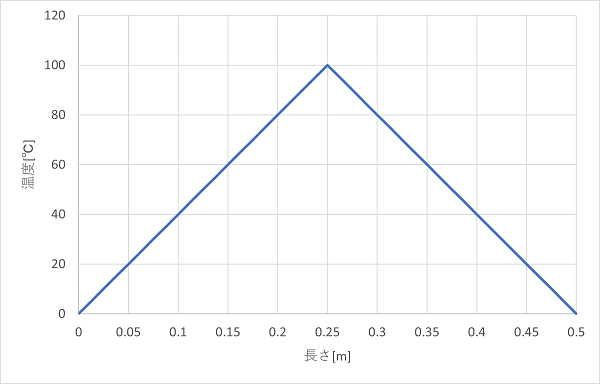
初期に、下図のような中央が 100 ℃ となるような温度分布が与えられているとします。

解析モデルは、９個のノードからなる熱回路網モデルで、ノードは等間隔に配置されています。

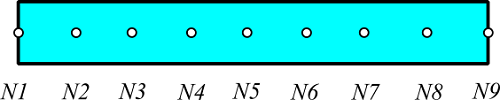
両端のN1、N9は０ ℃に固定され、隣り合うノードは熱伝導による熱抵抗で接続します。初期条件として各ノードに前述の温度分布に対応する温度を与え、CATTHMで非定常計算を行ないます。

このモデルは、次に示す1次元の非定常熱伝導方程式で解くことができます。

$$\frac{\partial T}{\partial t} = a \frac{\partial^2 T}{\partial x^2}$$

ここで、$T$：温度、$t$：時間、$x$：距離、$a$：熱拡散率（$=\lambda /(C_p \rho)$)、$\lambda$：熱伝導率、$C_p$：比熱、$\rho$：密度。

この方程式は、今回の条件のもとで、変数分離法を用いて解析的に解くことができ、以下のような理論解となります。

$$T =T_0 \sum_{n=1}^{\infty} \frac{8}{n^2 \pi^2} \sin(\frac{n \pi}{2}) e^{-a (n \pi / L)^2 t} \sin (\frac{n \pi}{L} x)$$

ここで、$L$：棒の長さ、$T_0$：中央の初期温度。

各ノードの温度の時間変化グラフを示します。

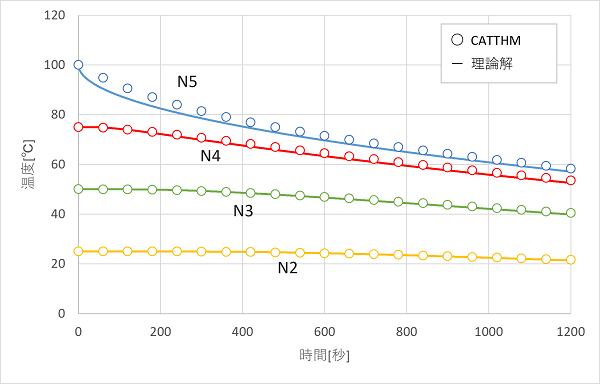
理論解を実線、CATTHMの結果を丸点で示しています。計算結果は、理論解と大体一致しており、時間とともに温度が下がっていく様子がわかります。

N5のみ初期に若干、計算結果の方が理論解より温度が高めに推移しています。これは、温度の空間分布をみると理解できます。

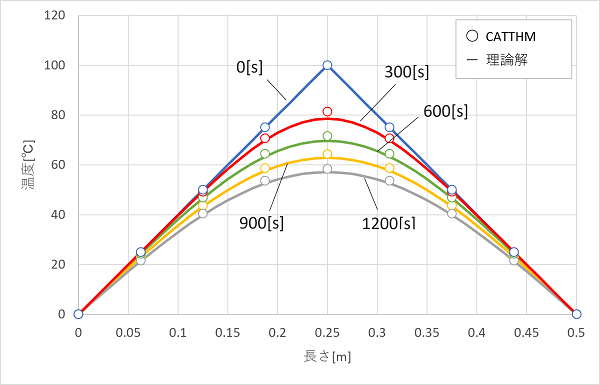
N5は中央 0.25 m 位置のノードです。初期に中央で最も温度が高い尖った山のような分布をしていますが、時間がたつと中央が丸みを帯びてきて温度低下していきます。その周りも徐々に温度が下がってきて、だんだんなだらかな山形状になっていきます。

初期段階で中央付近の丸みを帯びた温度分布をとらえるためには、もっとノードの数を増やす必要がありそうです。さらに分割数を上げて行けば理論解に近づきますが、そうすると分割数の多い差分法などと変わらなくなります。

しかし逆に言えば、このように少ないノード数でも、このくらいの分布を十分捉えることができると言えます。モデルの簡便さや計算時間の観点からも熱回路網法による解析は、簡単にサッと熱解析を行うには良い手法と考えられます。