両端支持梁（等分布荷重）の計算（断面２次モーメント指定）

等分布荷重による両端支持梁の計算

等分布荷重による両端支持梁の強度を計算します。

1. 分布荷重$w$、梁の長さ$l$を入力します。
2. 材質を選択するとヤング率$E$、密度$\rho$が自動で入力されます。値は適宜変更してください。
3. 自重による影響のありなしを選択します。
4. 断面２次モーメント$I$、断面係数$Z$、断面積$A$を入力します。
   断面２次モーメントと断面係数、断面積は以下のページで計算できます。
   →断面二次モーメントと断面係数の計算
5. 最大せん断力$Q$、最大曲げ応力$\sigma$、最大曲げモーメント$M$、最大たわみ$\delta$が計算されます。

※各物理量の単位に注意してください。

入力	分布荷重 $w$ [N/mm]
	長さ $l$ [mm]
	材質
	ヤング率 $E$ [GPa]
	密度 $\rho$ [kg/m3]
	自重	あり なし
	断面２次モーメント $I$ [mm4]
	断面係数 $Z$ [mm3]
	断面積 $A$ [mm2]
結果	せん断力 $Q$ [N]
	曲げ応力 $\sigma$ [MPa]
	曲げモーメント $M$ [Nm]
	たわみ $\delta$ [mm]

※断面２次モーメントと断面係数、断面積は以下のページで計算できます。
→断面二次モーメントと断面係数の計算

計算式

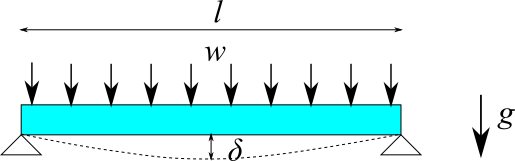
等分布荷重

両端が単純支持された長さ $l$ の梁に、等分布荷重 $w$ を作用させます。このときの諸量は以下のようになります。

最大せん断力（端部）

$$Q = \frac{wl}{2} $$

最大曲げモーメント（中央部）

$$M=\frac{wl^2}{8}$$

最大曲げ応力（中央部）
$$ \sigma = \frac{M}{Z}$$

最大たわみ（中央部）
$$\delta=\frac{5wl^4}{384EI}$$

自重

自重による影響は、自重を等分布荷重$w=\rho g A$として計算できます。重力加速度$g$は上図のように下向きにかかっているとします。

自重による影響を考慮する場合は、前述の等分布荷重に加えて計算します。

関連ページ

• 片持ち梁（集中荷重、断面２次モーメント指定、自重考慮）
• 片持ち梁（等分布荷重、断面２次モーメント指定、自重考慮）
• 両端支持梁（集中荷重、断面２次モーメント指定、自重考慮）
• 両端支持梁（等分布荷重、断面２次モーメント指定、自重考慮）
• 両端固定梁（集中荷重、断面２次モーメント指定、自重考慮）
• 両端固定梁（等分布荷重、断面２次モーメント指定、自重考慮）
  →断面２次モーメント、断面係数を指定するため任意の断面形状に対応できます。自重も考慮した計算ができます。
• 片持ち梁（集中荷重、矩形断面）
• 片持ち梁（等分布荷重、矩形断面）