ベルヌーイの定理

ベルヌーイの定理について解説します。

ベルヌーイ（Bernoulli）の定理は次の式で表されます。

$$\frac{1}{2}v^2+\frac{p}{\rho}+gz=const.$$

ここで、$v$：流速、$p$：圧力、$\rho$：密度、$g$：重力加速度、$z$：高さ

これは、運動エネルギー、圧力によるエネルギー、位置エネルギーの和が一定であるというエネルギー保存則を意味しています。

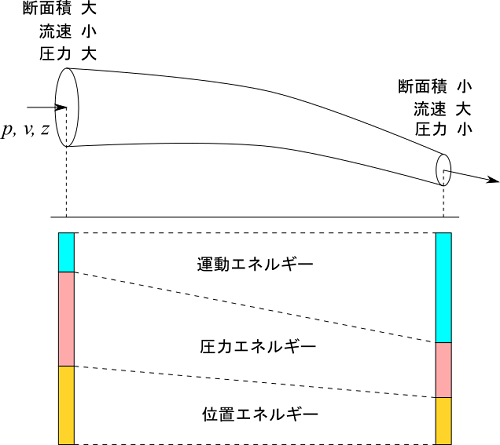
図のような管を流体が流れると、質量保存（流量保存）により断面積が大きいと流速が小さく、断面積が小さいと流速が大きくなります。この場合、ベルヌーイの定理より流速が大きい方が圧力が小さくなります。

※この式は厳密には、一様重力中での粘性を無視した完全流体でかつ、密度一定の非圧縮性流体の定常流れにおける流線上で成り立ちます。

ベルヌーイの定理の検証

CATCFDzeroで実際に流体解析をしてベルヌーイの定理が成り立つか確かめてみましょう。下図のようなｘ方向に長さ１で断面積が線形に変化するような管を考えます。

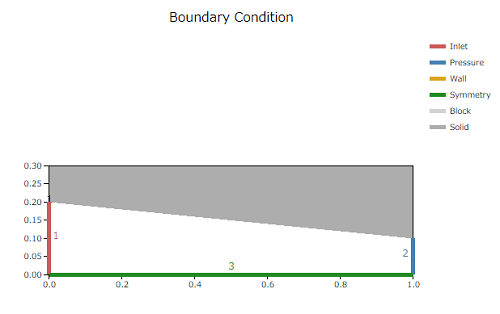
計算上y=0で対称境界条件としてハーフモデルにしています。左端から密度１の流体が流入してきた場合の流れ場を計算します。重力は無視して非圧縮の定常流の条件です。

速度と圧力の結果を以下に示します。

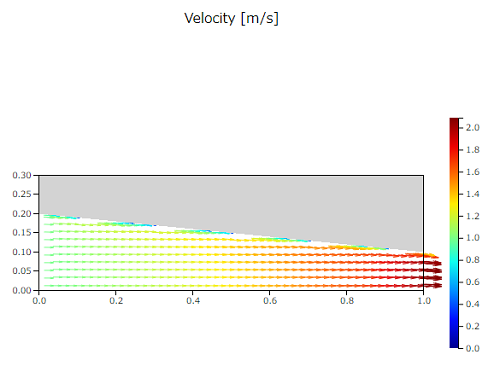
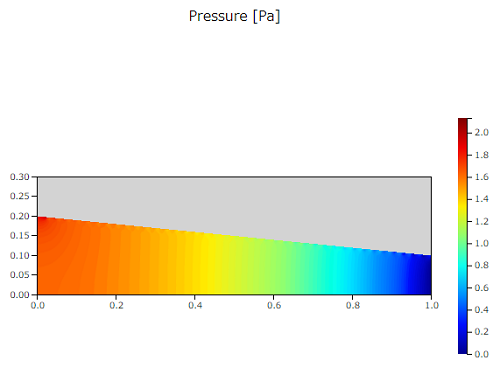
速度ベクトルを見ると速度の大きさは徐々に大きくなっていき、圧力は逆に小さくなっている様子がわかります。

ここで、y=0の管中央線における運動エネルギーと圧力によるエネルギーをグラフにすると、

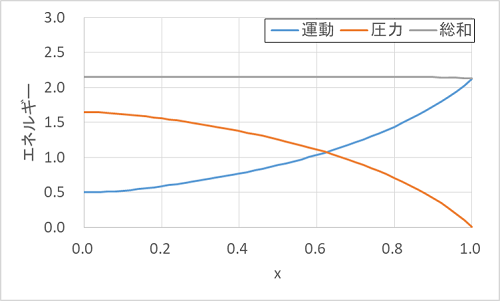
となり、総和がほぼ一定に保たれてベルヌーイの定理を満たしていることがわかります。

※この計算は、壁で粘性による摩擦損失があるため、厳密にはその分が加わっていますが、小さいので無視できます。