オンラインで無料で使える流体解析ツールCATCFDzeroに浮力計算の機能が追加されたので、検証計算を行ってみました。
目次
検証モデル
検証用のモデルは正方形の領域で、両サイドの壁に温度差を与え、自然対流による熱流れを計算します。
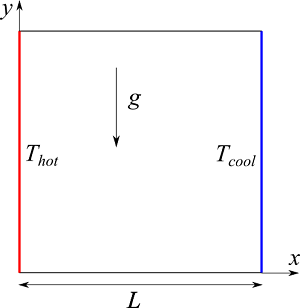
上下の壁は断熱で、y方向下向きに重力がかかっています。
自然対流を支配する無次元数はレイリー数 $Ra$ で、次式で表されます。
$$Ra=\frac{g \beta \Delta T L^3}{\nu \alpha}$$
$g$:重力加速度、$\beta$:体膨張率、$\Delta T$:温度差、$L$:代表長さ、$\nu$:動粘性率、$\alpha$:温度拡散率
レイリー数の違いにより自然対流の流れ場は違ってくるため、レイリー数を変えて計算を行います。
物性は空気とし、左右の温度差 $\Delta T$ は1[℃]で固定し、指定するレイリー数になるよう矩形のサイズ $L$ を変えることにします。メッシュ数は50✕50で、層流で計算しました。
検証結果
実測との比較
最初にKraneら[1]の実測と比較するために、$Ra=1.89 \times 10^5$ で計算を行いました。速度場と温度場の結果を以下に示します。
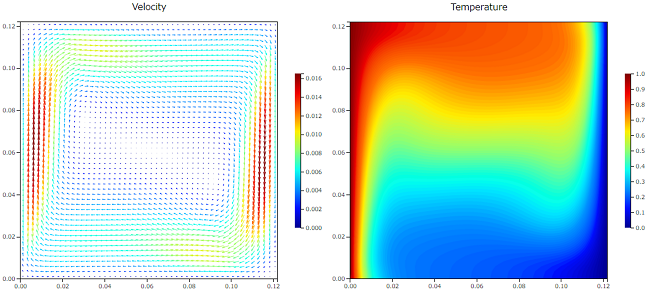
左側の高温壁で温められた空気が上昇し、天井に衝突した後右側の低温壁に移動します。右側の壁では空気は冷やされて下降していき、領域を循環する流れを形成しています。
実測との比較を下図に示します。これは、y方向の中央断面での速度のy方向成分 Uy のグラフです(速度と長さは比較のため無次元化してあります)。
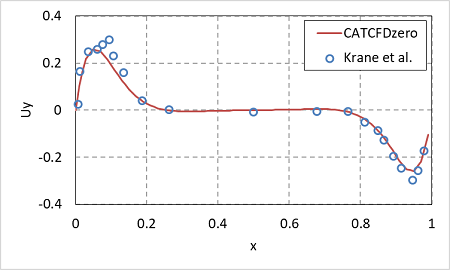
次の図は同じ断面の温度 T のグラフです。
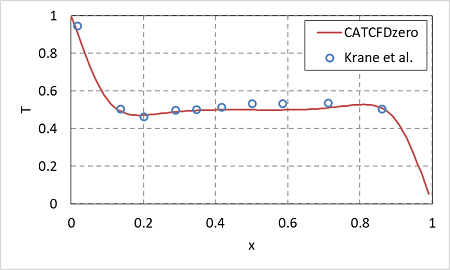
また、水平x方向の中央断面での速度のx方向成分 Uxを下図に示します。
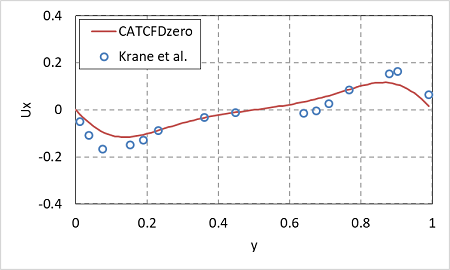
Uxは若干実測のピークの方が大きいですが、全体的な分布や値はだいたい一致していることがわかります。
レイリー数による違い
次に、レイリー数による違いを比較してみます。$Ra = 10^3, 10^4, 10^5, 10^6$ の4パターンで計算した結果を載せます。
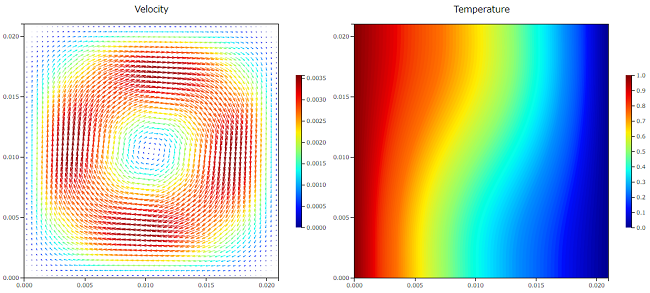
$Ra=10^3$
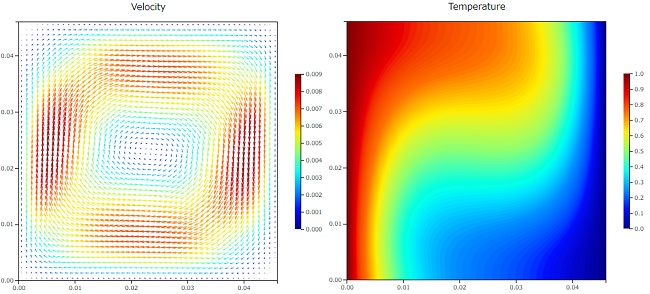
$Ra=10^4$
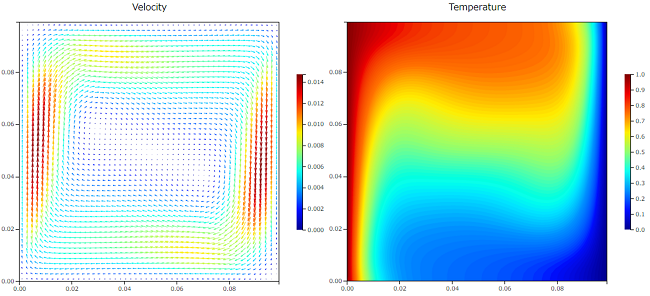
$Ra=10^5$
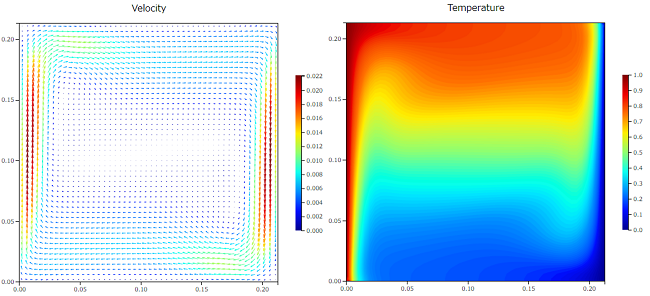
$Ra=10^6$
$Ra$ が小さいと全体的に大きな循環した渦が形成されていますが、$Ra$ が大きくなると温度境界層が薄くなり温度固定壁面に集中していく流れとなっています。
Davisの文献[2]の結果との比較を以下に示します。これは、x方向の中央断面でのUxの最大値とy方向中央断面でのUyの最大値について、それぞれ比較したものです。
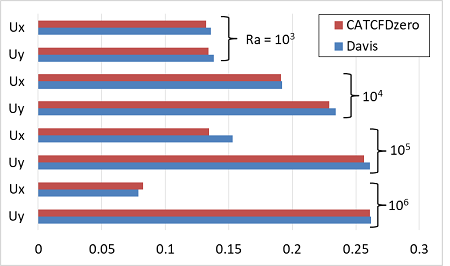
各レイリー数で速度の値はよく一致しています。
まとめ
今回はCATCFDzeroの浮力計算機能の検証を行ってみました。基礎的な検証ですが、実測や他の文献と比較して同等の結果が得られていることが確認できました。
自然対流は、部屋の中の温熱環境をはじめ様々なところで重要となってくる計算です。CATCFDzeroはこれらの計算がオンラインで無料で簡単にできますので、ぜひ使ってみてください。
