目次
はじめに
流体には様々な定理や法則があります。その代表のひとつがベルヌーイの定理です。
ベルヌーイの定理はあまりにも有名なので、流体現象は何でもベルヌーイで説明してしまうという風潮があるようです[1][2]。そこで今回は、文献の中の例を参考に2つの題材について流体解析で検証を行ってみたいと思います。
※いちおう念の為ですが、文献も本ページでもベルヌーイの定理自体を否定しているわけではありません。
ベルヌーイの定理とは
ベルヌーイの定理の詳細は以下のページを参照してください。
ベルヌーイの定理は流体に関するエネルギー保存則を表しています。
$$\frac{1}{2}\rho v^2+p+\rho gz=const.$$
ここで、$v$:流速、$p$:圧力、$\rho$:密度、$g$:重力加速度、$z$:高さ
単純に式だけを見ると「流速の大きい所では圧力が低い」ということになります。
このことをもとに、身の回りの現象で、流速が速いところは単純に圧力が低くなるという誤解が起こり、何でもベルヌーイの定理で説明しようとする誤謬が生じているようです[1][2]。
ベルヌーイの定理は、粘性のない完全流体の同一流線上で成り立ちます。したがって、粘性によるエネルギー損失が大きい系や外部からエネルギーが供給されるような場合は、この定理自体が成り立ちません。また、同一流線上に無い全く異なる流れ場に対して、ベルヌーイの定理により速度と圧力の関係を議論することはできません。
例題
今回は簡単な理科実験が出来るもの2つを題材に検証してみます。
霧吹き
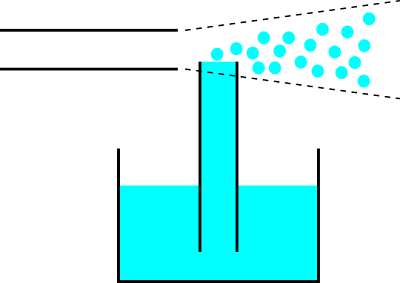
水を入れた容器にストローを刺し、もう一つのストローで先程のストローの先端に息を吹きかけると、水が吸い上げられ霧吹きのようになる[1][2][3]。
コの字の紙
コの字型の紙と机の隙間にストローで息を吹きかけると、紙が机に押し付けられる[4]。

これら2つは、一般的に「ストローから出た息の噴流がまわりより高速であるため、ベルヌーイの定理により噴流が低圧になり、水を吸い上げたり、紙を引きつけたりする」と説明されています。実際、ネットで検索するとそのような説明が多く見られます。しかし、この説明が誤解であると先の文献では指摘されています。
噴流の圧力
個々の事例の前に、まずは自由噴流の流れのようすから、流体解析で検証してみます。
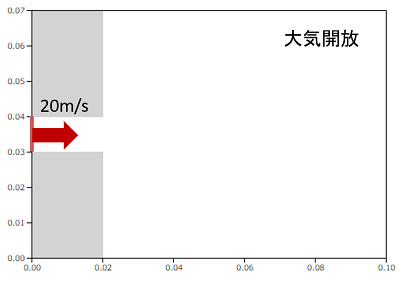
流体解析は本サイトのCATCFDzeroを使用して行います(※)。
モデルは下図のように、10mm径のストローから20m/sで大気圧中に空気を噴出します。
速度分布は次のようになります。
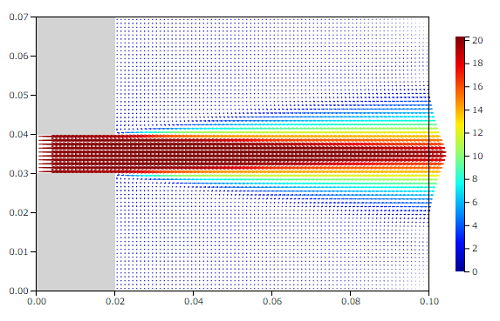
速度ベクトル[m/s]
20m/sで噴出された空気は、まわりの空気を取り込みながら(エントレインメント: entrainment)、粘性の影響により徐々に流速を下げていきます。下図は流線と流速ですが、まわりの空気を取り込んでいくようすが分かります。
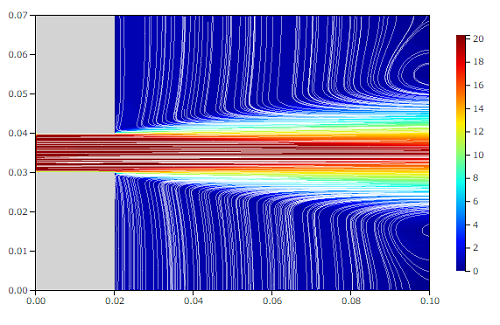
流線と速度コンター[m/s]
次に圧力分布(静圧)です。
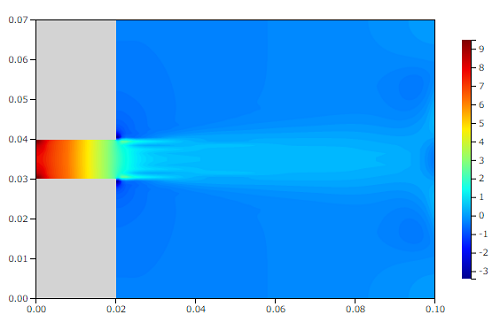
圧力[Pa]
噴流は周囲の大気よりも高速ですが、噴流部が特にまわりに比べ低圧になっているようすは見られません。ストローから吐出されたあとはすぐに大気圧(0Pa)に近づいています。
つまり、圧力分布を見ても「噴流の高速部でまわりに比べ低圧になっている」という解釈は成り立たないことが分かります。
※CATCFDzeroは非圧縮性、定常、2次元の流体コードのため、圧縮性や非定常性、3次元性が顕著な場合は、分布や絶対値が実際と異なる場合があることにご注意ください。
霧吹き
霧吹きの原理
文献[2]によると、霧吹きの誤った解釈は、「下図の噴流のA点の圧力がベルヌーイの定理により低下するため、水を吸い上げる」というものです。

これは前述の自由噴流の結果のとおり、噴流の高速部で圧力は低下しないことからも、この解釈が明らかに誤っていることがわかります。
文献[2]では、正しい原理として次のようなものをあげています。
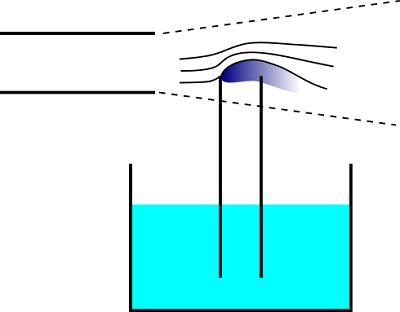
「噴流の中に吸水パイプを挿入した場合、パイプ上端の前縁で剥離が生じ、流れが加速される。これにより、剥離部の圧力が低下し水を吸い上げる」というものです。この部分では局所的であることから流速と圧力の関係をベルヌーイの定理を用いて説明しています。
霧吹きモデルの流体解析
これも、流体解析で検証してみます。下図のようなモデルを使います。
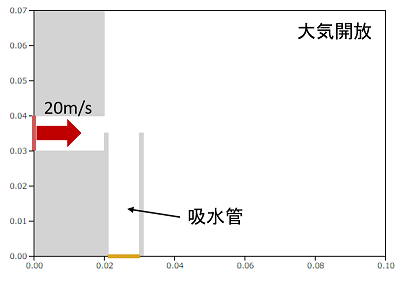
10mm径のストローの出口すぐのところに、径の半分の高さまで吸水用のストローを差し込みます。自由噴流と同じ様に20m/sの流速で空気を大気中に噴出させます。ここでは水は考慮せず、吸水管内の圧力を見ることにします。
速度場は次のようになりました。
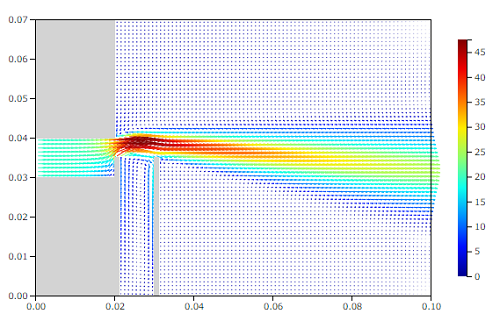
速度ベクトル[m/s]
噴出口から出てくる流れは、吸水管の上端に回り込み、その端面で剥離しています。その時、加速され速度は倍以上の47m/sほどになっています。吸水管を過ぎた流れは、また噴流のようになり下流へ流れていきます。このときの圧力分布を下図に示します。
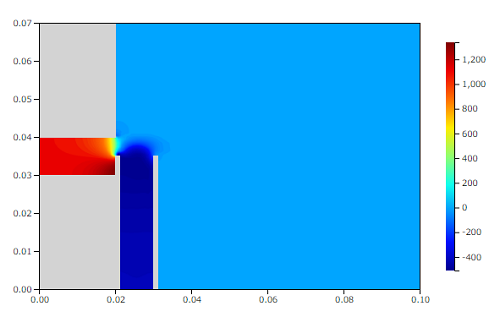
圧力[Pa]
吸水管上端で剥離し加速している部分で、圧力が低下していることが分かります。ここの圧力は-500Paほどになっており、吸水管内部が負圧になっています。これらの結果は、文献[2]の正しい原理と同様になっていると考えられます。
なお、吸水管を過ぎた噴流はまたすぐに大気圧に戻っています。
ちなみに、文献では吸水管上部の流速は、上流側の流速の1.3倍程度となっていますが今回の結果は2倍以上になっています。これは3次元の円管の場合、一部はパイプの側面に沿って流れるものがあるためだと考えられます。したがって、今回の2次元計算では、流速および圧力低下が3次元計算に比べやや過大になっている可能性がありますが、定性的には再現できているのではないかと思います。
霧吹きが起こらない条件
次に吸水ストローを少し下げて、噴出口の下面に吸水管の上端が来るようにした場合を計算してみます。文献[3]では、この場合は水の吸い上げが起こらず霧吹き現象が起きない条件となっています。文献[3]には動画もあるので、見てみてください。
流れ場は、
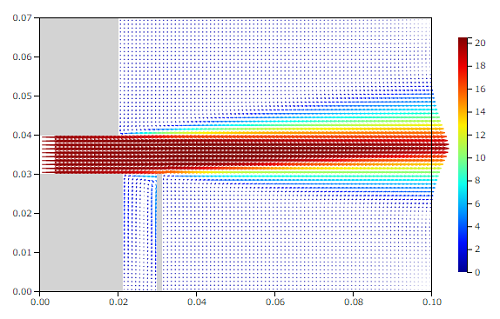
速度ベクトル[m/s]
のようになりました。噴流は吸水管の部分では特に加速することもなく、きれいに噴出しています。
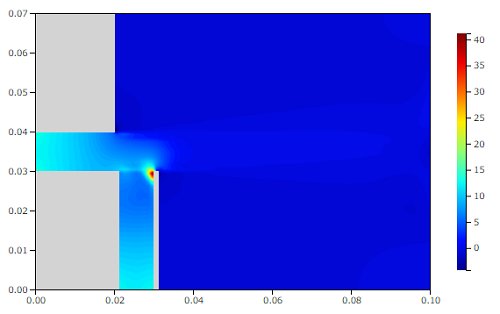
圧力[Pa]
圧力分布も吸水管上端で圧力低下は見られず、吸水管内部も負圧になっていません。したがって、この条件では水が吸い上げられず、霧吹きは起きないと言えます。
もし、ベルヌーイの定理の誤った解釈のように、噴流自体の低圧化によるものだとすると、この条件でも水の吸い上げが起きそうですが、実際にも計算でもその様な結果にならないことが分かります。
コの字の紙
次に、コの字の紙の例を検討してみます。上記の写真のように紙をコの字状に両端を折り曲げて机の上に置きます。紙と机の隙間にストローで息を吹きかけます。すると、紙が机に吸い付きます[4]。
これも噴流の速度が大きいため、噴流自体が低圧になるというベルヌーイの定理の誤った解釈がされているようです。
コの字の紙の流体解析
こちらは、次のようなモデルで流体解析を行ってみます。2次元モデルです。
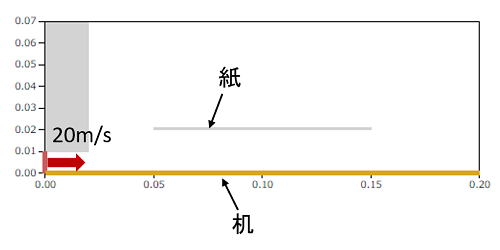
同じく10mmのストローから20m/sの噴流を出します。紙を途中に置きます。領域の下端は壁(机)ですが、それ以外は大気開放です。
速度場の計算結果は次のようになります。
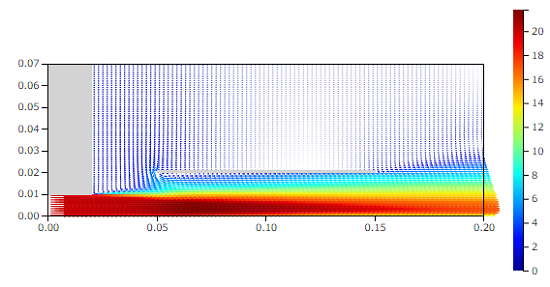
速度ベクトル[m/s]
噴流は下端の机に沿って流れていきます。噴流はまわりの空気を取り込んで幅が大きくなりますが、途中に紙があるのでここで抵抗になっていそうです。圧力分布は、
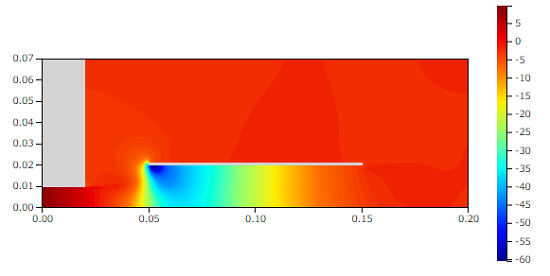
圧力[Pa]
のようになっています。ストローから出た噴流はいったん大気圧に近づきますが、紙の入口で急に圧力が低下しています。この圧力低下は紙面の入口側の端点で一番大きいようです。
この部分の流れ場を拡大してみます。
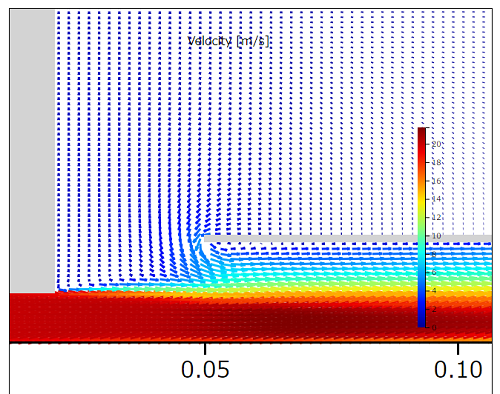
紙入口付近の拡大:速度ベクトル[m/s]
噴流に向かって流れる周囲の空気が紙の端点で剥離していることがわかります。この部分での圧力低下が顕著になっています。またこの剥離で流路が狭められ、噴流は21.7m/sに流速が増加しています。局所的にベルヌーイの定理を適用すれば、この部分は速度増加に伴い圧力が低下する一因となりえます。
紙と机の間の圧力は大気圧に比べ負圧になっており、これは徐々に回復し紙を出ると大気圧に戻っています。このとき、紙の反対側(上面)は大気圧のままなので、紙には机に向かう力が働き、机に吸い付くようになると考えられます。
文献[4]では周囲空気の取り込みについて明確に書かれていませんが、はく離による低圧化の説明がなされています。
紙と机の幅が広い場合
追加で、紙と机の幅をもっと大きくとった場合も検証してみました。
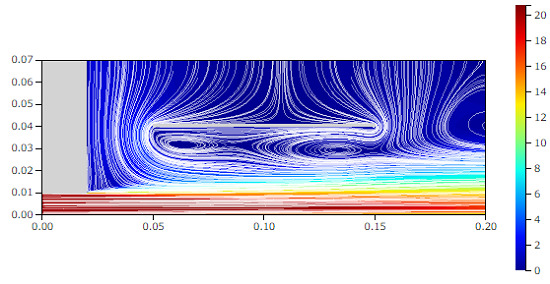
流線と速度コンター[m/s]
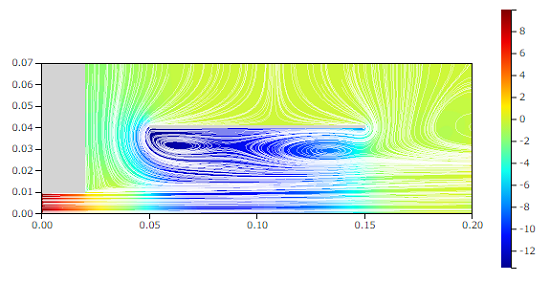
流線と圧力[Pa]
この場合も紙と机の間は負圧になっていることがわかります。流れ場を見ると、やはりエントレインメントによる周囲空気の取り込みが、紙があることによって阻害され、圧力を下げていると言えそうです。文献[5]の動画を見ると、噴流からかなり離れたところにある板も噴流に吸い寄せられる、というのがよく分かります。
いずれにしても、この現象を短絡的に噴流が高速だから圧力が低下するという誤ったベルヌーイの定理の使い方で説明するのは間違いであると考えられます。
なお、今回のモデルは2枚の紙の間に息を吹いた時に、紙どうしが引きつけ合うという現象[1]にも適用できると思います。
まとめ
今回はベルヌーイの定理を使った流体現象の解釈について、文献をもとに流体解析で検証を行ってみました。定理や法則など様々なものが流体力学にはありますが、誤った使い方や教科書に書いてあることだけを鵜呑みにして使っている例が多いと思います(自戒の念をこめて)。実測やシミュレーション、解析などで、速度や圧力などの分布を見て総合的に判断することによって、流体や物体に働く力学的現象をきちんと確かめた上で使っていきたいものです。特にひとつの定理や法則の名称だけで現象全体を表そうとするのには注意が必要です(再度、自戒の念をこめて)。
また、簡単に見える身近な現象でも、形が異なったり、条件がちがったりすると、作用する力学的メカニズムが異なる可能性があるので、その点もご注意ください。ここにあげた例も、条件によっては違うメカニズムが働いているかもしれません。
なお、今回の題材は簡単に実験することができるので、自由研究にご家庭でも楽しんでみてください。
また、当サイトのオンライン流体解析ツールCATCFDzeroを使うと、これらの解析がわずか数分でできるので、電卓感覚でぜひ使ってみてください。