円筒の熱通過と表面温度を計算する
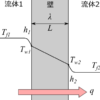
円筒壁に仕切られた流体１と流体２の間の熱通過と壁の表面温度を計算します。
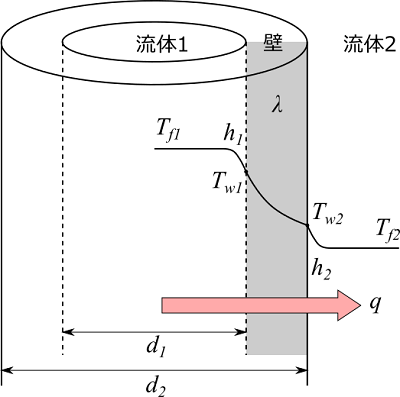
- 円筒の外径、内径を入力します。
- 流体１、流体２の温度、熱伝達率を入力します。
- 壁の熱伝導率を入力します。
- 壁の表面温度、通過熱量、全体の熱通過率が出力されます。
※通過熱量、熱通過率は円管の長手方向の単位長さあたりの量として計算されます。
※通過熱量$q$は流体１から流体２への方向が正として出力されます。
※壁表面温度を流体温度に固定したい場合は、流体の熱伝達率に大きな値 1e10 を入力してください。
※流体の熱伝達率は、空気・水に対する自然対流、強制対流から選ぶことが出来ますが、流れの性状や流速により実際にはかなり幅があります。入力された値はあくまで代表的なオーダーの値なので適宜調整してください。以下のページから算出することもできます。
スポンサーリンク
計算式
流体１から流体２への円管単位長さあたりの全体の熱通過率$K$は、
$$\frac{1}{K} = \frac{1}{h_1 d_1}+\frac{1}{2\lambda} \ln{ \frac{d_2}{d_1}} + \frac{1}{h_2 d_2}$$
で表されます。よって、流体１から流体２への円管単位長さあたりの通過熱量$q$は、
$$q=K \pi (T_{f1}-T_{f2})$$
で計算できます。また、流体１と壁との間の通過熱量は
$$q=h_1 \pi d_1 (T_{f1} - T_{w1})$$
壁と流体２との間の通過熱量は
$$q=h_2 \pi d_2 (T_{w2} - T_{f2})$$
と書け、それぞれの通過熱量は同じであることから、壁の表面温度$T_{w1}$、$T_{w2}$が計算できます。
平板の熱通過の計算は次のページです。
熱通過と壁の表面温度の計算ができるページです。壁に仕切られた流体１と流体２の間の熱通過と壁の表面温度を計算します。流体の温度、熱伝達率、壁の熱伝導率、厚みを入力すると壁の表面温度、熱流束、全体の熱通過率が出力されます。