オンラインで無料で使える流体解析ソフトCATCFDzeroでキャビティ流れ解析の検証を行ってみます。キャビティ流れは矩形の領域で上面が速度規定された流れです。
目次
検証モデル
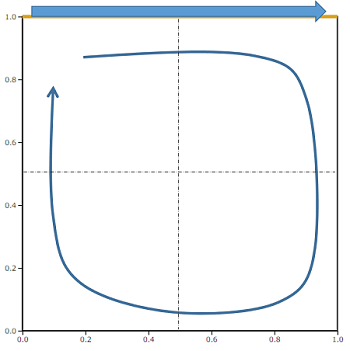
検証用のモデルは正方形の領域で、上端の壁面に速度を与えます。
流れの特性を表すレイノルズ数 Reは、次式で与えられます。
$$Re = \frac{\rho UL}{\mu}$$
$\rho$:密度、$U$:壁面速度、$L$:矩形の幅、$\mu$:粘性係数
$\rho=U=L=1$ とすると、粘性係数は
$$\mu = \frac{1}{Re}$$
で表されます。計算では指定するRe数となるように粘性係数を変更して計算します。
メッシュは100×100の均等メッシュに対して、ソリッド機能を使用して壁面近傍のメッシュを一段階細分割しています。流れは層流で、対流項の差分スキームは2次風上差分(※)を使っています。
※2次風上差分スキームは拡張機能で使用することができます。
検証結果
速度場の比較
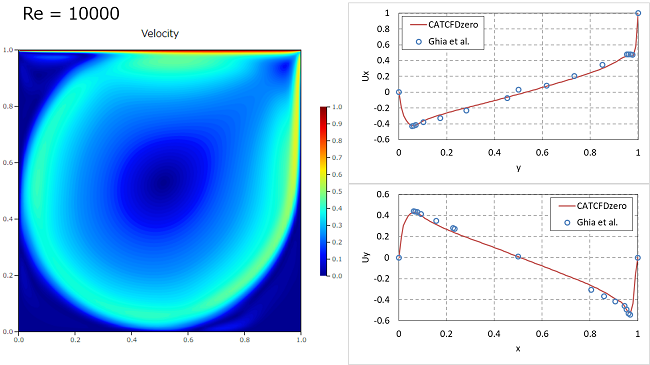
レイノルズ数 Re=100, 1000, 5000, 10000の4パターンを比較してみます。速度コンター図と、領域中央の鉛直y方向における速度Uxおよび水平x方向の速度Uyのグラフを示します。速度はGhiaら[1]の結果と比較しています。
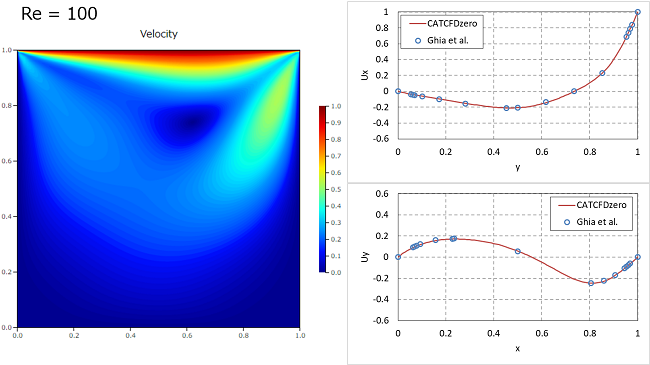
$Re=100$
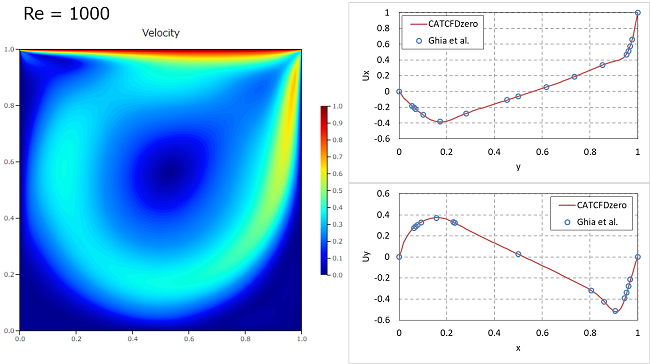
$Re=1000$
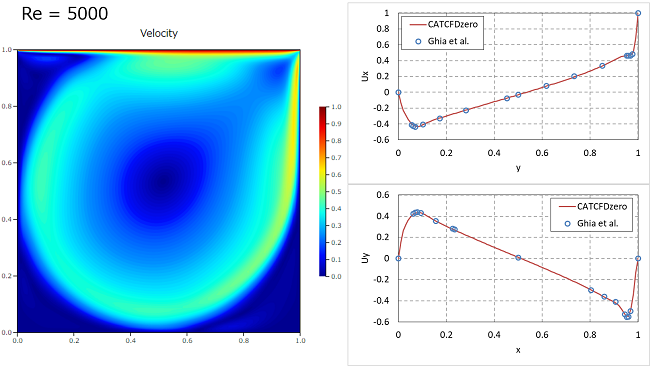
$Re=5000$

$Re=10000$
Re数が大きくなるにつれて、大きな循環した流れになることがわかります。また壁面付近に急峻な速度境界層ができていきます。速度場はGhiaらの結果とよく一致しています。
渦の比較
次に各Re数で形成される渦を比較してみます。下図は流線を表示したものです。
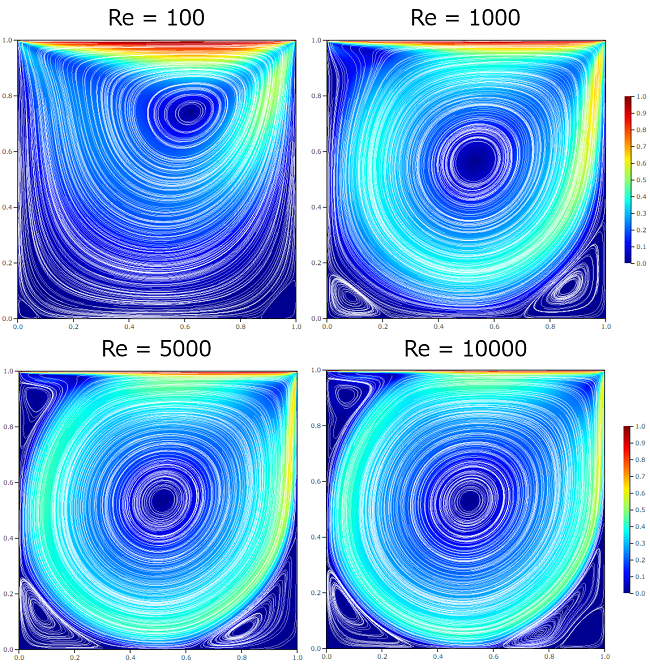
各Re数とも上端面の速度によって大きな渦が形成されています。Re=100では渦の中心は右上にありますが、Re数が大きくなると領域中央に位置していきます。またRe数が大きくなると領域の角に2次渦が形成されていくのがわかります。Re=10000では右下角にさらに独立した渦が見られます。
差分スキームの比較
差分スキームの比較を行ってみます。下図はRe=10000での1次風上差分と2次風上差分の比較です。
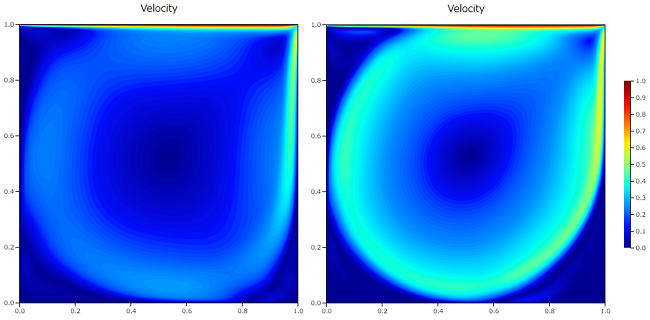
速度コンター図(左:1次風上、右:2次風上)
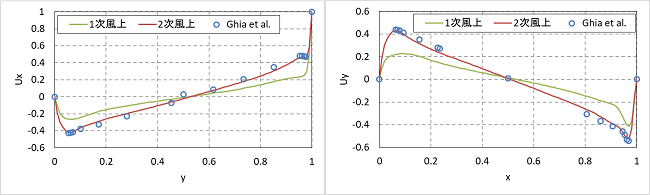
中央断面での速度(左:Ux、右:Uy)
1次風上は速度がなまってしまいピークも小さくなっています。1次風上は1次精度、2次風上は2次精度の差分スキームです。1次精度の風上差分は数値拡散により解が拡散してしまう傾向にありますが、計算は安定で収束性もよいのが特徴です。2次精度のスキームは解がシャープに得られますが、計算が不安定だったり収束性が悪かったりします。問題によって使い分けるとよいでしょう。
まとめ
今回はCATCFDzeroでキャビティ流れの検証を行いました。キャビティ流れは流体解析のベンチマークとしてよく用いられる基礎的な問題です。Re数による流れ場の変化や他の文献と比較して同等の結果が得られていることが確認できました。
CATCFDzeroはこれらの計算がオンラインで無料で簡単にできますので、ぜひ使ってみてください。
