Cantera：着火遅れ時間の計算

※Canteraバージョン：3.0.0

Canteraで着火遅れ時間を計算してみる。n-Heptaneの空気中での燃焼における着火遅れ時間を計算する。

# condition
temp = 1000.0
p = 1.3e6
phi = 1.0

初期温度1000K、圧力1.3MPa、当量比1.0の条件で計算する。

# define gas state
gas = ct.Solution('LLNL_heptane_160.yaml')
gas.TP = temp, p
gas.set_equivalence_ratio(phi, 'nc7h16', 'o2:1.0, n2:3.76')
states = ct.SolutionArray(gas, extra=['t'])

n-Heptaneの反応メカニズムは、LLNLの縮約されたメカニズム（化学種160、反応式1540）[M1]を使う。states=SolutionArrayは、後で時間を記憶しておくための配列を準備している。

# define reactor
r = ct.IdealGasReactor(contents=gas, name='Batch Reactor')
sim = ct.ReactorNet([r])

理想気体の定容容器の反応器モデル（IdealGasReactor）を使う。

# time condition
tend = 0.1  # end time
dt = 1.0e-6 # time step

計算の終了時刻を0.1秒、時間刻みを1μ秒とする。

# time loop
for time in np.arange(0, tend, dt):
    sim.advance(time)
    states.append(r.thermo.state, t=time)

時間積分をする。sim.advanceはその時刻まで計算するという関数。states.appendで先ほど用意した配列に、結果と時間を格納している。

# ignition delay time
time_igd = states.t[np.argmax(np.diff(states.T))]
print('\n Ignition Delay Time: {:.3e} micro sec'.format(time_igd * 1e6))

time_igdに着火遅れ時間が入る。着火遅れ時間は、温度の勾配（diff）が最大（argmax）となる時刻で計算している。他にも、温度がある値以上上昇した時刻や、ある化学種がピークとなる時刻などで算出する方法もある。

#plot
plt.plot(states.t, states.T)
plt.xlim(0, 0.01)
plt.xlabel('Time [sec]')
plt.ylabel('Temperature [K]')
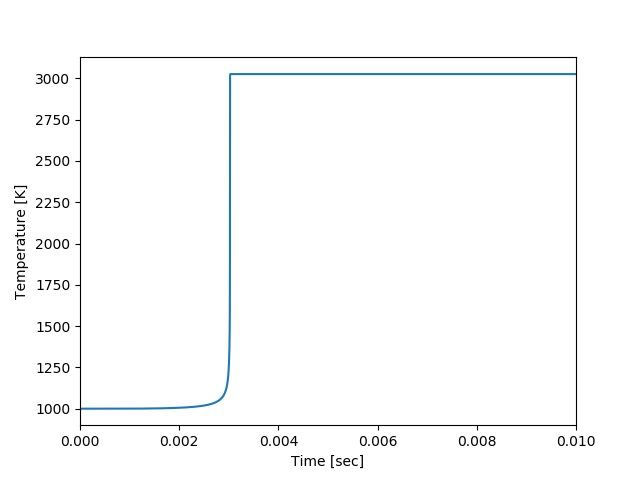
plt.show()

最後に、時間に対する温度のグラフを表示する。急激な温度上昇がある時刻が着火遅れ時間となる。

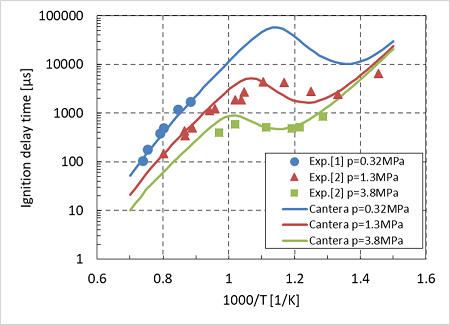
圧力と温度を変化させて着火遅れ時間を計算し、実測[1][2]と比較したグラフを載せておく。

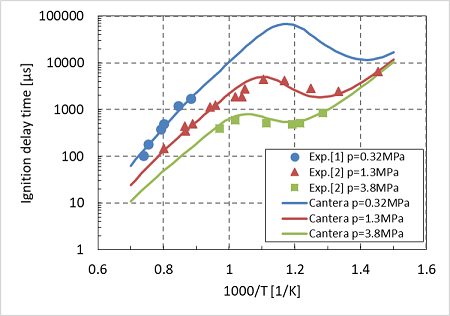
LLNLではn-Heptaneのより詳細なメカニズム（化学種 654、反応式4846）[M2]が公開されているので、こちらでも計算してみる。

参考文献

反応メカニズム：

[M1] "n-Heptane, Reduced Mechanism", Lawrence Livermore National Laboratory
https://combustion.llnl.gov/archived-mechanisms/alkanes/heptane-reduced-mechanism

[M2] "n-Heptane, Detailed Mechanism, Version 3.1", Lawrence Livermore National Laboratory
https://combustion.llnl.gov/mechanisms/alkanes/n-heptane-detailed-mechanism-version-3

実測値：
[1] Ciezki, H. K.; Adomeit, G. Shock-tube investigation of self-ignition of n-heptane-air mixtures under engine relevant conditions. Combust. Flame. 1993, vol. 93, p. 421–433.

[2] Heufer, K. A.; Olivier, H. Determination of ignition delay times of different hydrocarbons in a new high pressure shock tube. Shock Waves, 2010, vol. 20, p. 307–316.