多孔質媒体の圧力損失

多孔質媒体の圧力損失の計算

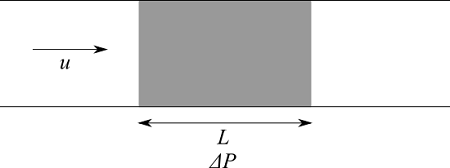
多孔質媒体（porous medium）を流体が通過するとき、圧力損失 $\Delta P$ が生じます。圧力損失はDarcy則による粘性項（viscous term）に、慣性項（inertial term）を加えたForchheimerの式がよく使われます。

流体解析ソフトなどでは(1)式のように速度 $u$ の係数を直接指定する方法か、(2)式のように粘性係数 $\mu$、流体密度 $\rho$ を用いて係数を指定する方法で表す場合が多いです。

$$\frac{\Delta P}{L} = K_v u + K_i u^2 \tag{1}$$

$$\frac{\Delta P}{L} = k_v \mu u + \frac{1}{2} \rho k_i u^2 \tag{2}$$

ここで、$u$ は流体の速度、$L$ は多孔質媒体の長さ。それぞれ、右辺第１項が粘性項、第２項が慣性項です。

ここでは係数を入力して多孔質媒体を流体が通過するときの圧力損失を計算します。式を選択し、流速、長さ、係数、物性値を入力してください。圧力損失が計算されます。（デフォルトの粘性係数、密度は20℃の空気の値です。）