目次
はじめに
オンラインの流体解析ツールCATCFDzeroでは、2次元の流体解析を行うことができます。一方で、私たちは3次元空間で生活しているため、通常目にする流体の流れも3次元です。では、流体解析での2次元、3次元の違いはどのようなものでしょうか?
物体を過ぎる流れ
3次元はX-Y-Z軸からなる座標系で表される空間で、2次元とはX-Y軸からなる平面で表されます。
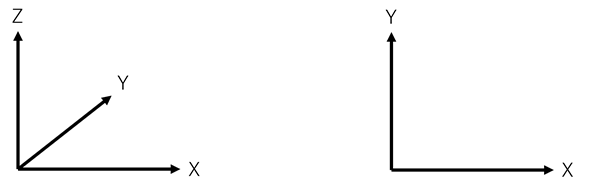
3次元空間では流体の流れも3次元で、位置も速度も3方向の成分を持っています。これを2次元で表すことは完全にはできません。
たとえば、3次元で円筒のような物体を過ぎる流れを考えてみます。
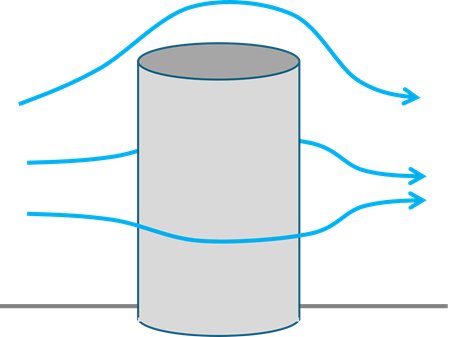
円筒の前面から流れてくる流体は、円筒の側面で手前と奥行き方向に分かれて流れます。また、円筒の上部を通過する流れもあります。
これを円筒の中央断面で切った2次元平面で表してみます。円筒の前面から流れてくる流体は、2次元のため奥行き方向には回り込むことができません。そのため、円筒の上部を回り込む流れとなります。
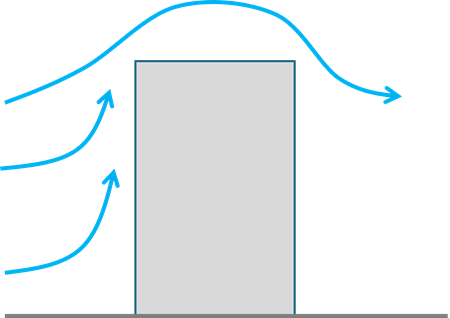
つまり、この例のような3次元の物体を通過する流体解析を2次元平面で行うと、物体の上部を通過する流量が多い結果となってしまいます。
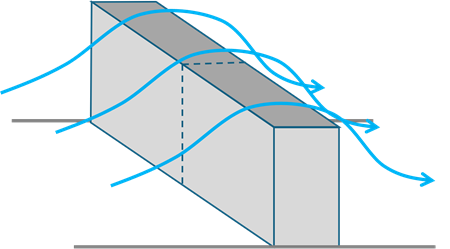
一方で、流路幅全体に横たわる長い角柱を過ぎる流体は、奥行き方向のどの断面でも似たような流れとなり、この場合は2次元平面で解析を行っても、実際の流れを模擬することができます。
管内流れ
パイプなどの単純な管内流れを考える場合でも2次元と3次元では注意が必要です。
3次元で下図のような断面積が変化する管を考えます。

菅の断面積は直径Dの2乗に比例します。つまり流量Qは直径Dの2乗に比例します。
一方、2次元では断面積は直径Dに比例し、流量Qも直径Dに比例します。

したがって、流速U1がどちらも同じだとすると、流速U2は3次元に比べ2次元では小さくなります。
このように3次元の管を2次元で表現した場合、流速の絶対値を評価するには注意が必要です。
容器への流入
次に、細い流入口から容器の中に流体が流入する場合を考えてみます。
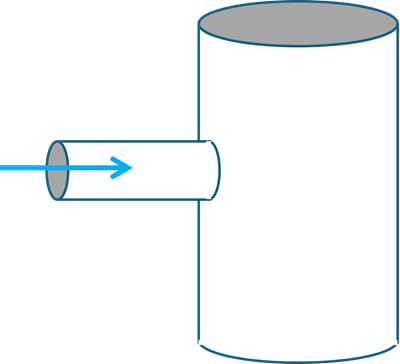
これを2次元で表すと、流入口を通る平面で計算することになります。
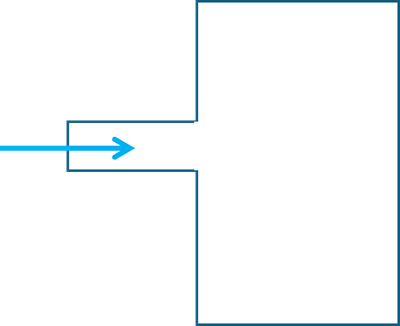
流入口から容器に入った流れは、実際は3次元的に奥行き方向にも流れますが、2次元解析の場合はその平面内でしか流れない結果となります。この場合、もし境界条件として同じ流入速度を与えると、2次元解析の方が容器内の流速が相対的に大きい結果になります。
※流量比を合わせるため容器の体積(2次元では断面積)に対する流量を調整しようとすると、今度は流入速度が小さくなります。
上記の2次元断面は、次のようなスリット状の流入口を持つ容器を再現するのに適しています。
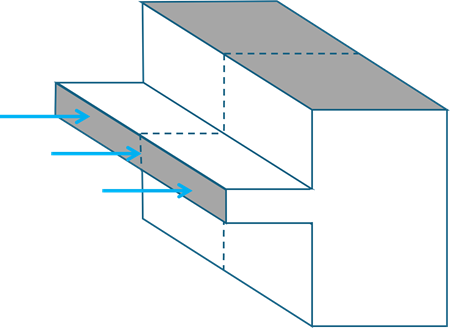
これだと奥行き方向に同じような流れとなり、2次元解析でも実際と同等の流れ場を得ることができます。
※ただし、容器の内部が3次元的な構造をしていると容器内の流れが変わってきます。
2次元流体解析の使いどころ
2次元的な形状
2次元の流体解析は、並進対称性を仮定した計算になっています。並進対称性とは奥行き方向には、同じ状態が続いていることを表します。つまり、奥行き方向にどの断面を切っても流れが変わらない(金太郎飴のような)状態です。
したがって、奥行き方向に同じ形状をしたものでは、2次元解析の結果は3次元と同様になり、十分評価できます。
一方で、3次元的に複雑な形状をしているものをある断面で切って2次元解析を行う場合は、注意が必要です。奥行き方向の流れ場がどのようになるか、3次元性はありそうか予想しながら結果を評価する必要があります。
計算コスト
3次元空間を厳密に再現するには、3次元の解析を行わなければなりません。もちろんそれができるに越したことはありません。しかし、3次元解析を行うには、高額な解析ソフトが必要で、計算設定に時間を費やしたり、計算機での計算時間が多くかかるなど、かなり計算コストがかかります。
その点、2次元解析だと比較的短期間、低コストで計算結果を得ることができるメリットがあります。特にCATCFDzeroであれば無償で簡単に計算を行うことができます。
流体可視化のファーストステップ
2次元的な形状であれば2次元解析で十分です。また、3次元的な形状でも、まずはざっくりした流れ場を把握するため可視化してみる、という目的で役に立ちます。
さらに、2次元解析で形状違いや条件違いなどのあたりを付けておいてから、最後に3次元解析で確認するといった使い方をすれば、効率的に解析業務を行うことができます。
「2次元解析は3次元を再現できないから使えない」と判断する前に、2次元解析と3次元解析の違いを理解したうえで、2次元解析のメリットを生かして活用していくと解析業務の幅が広がります。
