今回はPythonで多目的最適化を行ってみます。
目次
最適化
製品設計などを行う際に性能をこれくらいにしたいなど、目的を持って開発を行います。そのために、様々な設計パラメータを決める必要があります。当然、設計パラメータは複数ありますし、目的も複数存在します。さらに、コストはこれ以下にしなければならないとか、部品のサイズの上限が決まっているとか、制約も多く存在します。
これらを解決するために、最適化という技術計算を行います。ここでは、複数の目的が与えられたときに適用される多目的最適化を取り上げます。
多目的最適化
簡単な例題として、以下の問題を解いてみます。
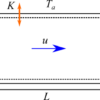
空気の出口温度が大きく、圧力損失が小さくなるように、円管の形状を決めたい。円管の形状を決めるには、長さと直径を変えることができる。なお、管の厚みは5mmとする。
管長さと直径をどのように決めればよいか?ただし、管の質量が80kgを超えないようにしたい。
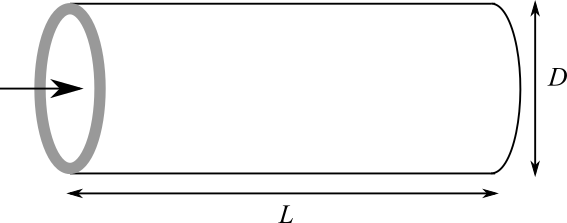
この問題で、目的となるのは、出口温度を大きく、圧力損失を小さく、の2つです。また、設計パラメータは、管の長さと直径の2つあります。さらに、管の質量が80kgを超えないという条件が課せられています。
目的が2つあるため、多目的最適化となります。この目的のことを目的関数と言い、設計パラメータのことを設計変数と言います。そして、満たすべき条件は、制約条件と呼ばれます。
設計変数はある範囲で変更できるものとすると、最適化の条件は次のように整理できます。
目的関数
- 出口温度最大化
- 圧力損失最小化
設計変数
- 管の長さ(0.1~10m)
- 管の直径(0.1~1m)
制約条件
- 管の質量が80kg以下
Platypus
ここでは、Pythonを使って多目的最適化を行ってみます。Pythonには、オープンソースのライブラリがたくさんありますが、多目的最適化を行うことができるオープンソースライブラリのPlatypusを使うことにします。
Platypusの公式サイト:https://platypus.readthedocs.io/
PlatypusのGitHub:https://github.com/Project-Platypus/Platypus/
多目的最適化には、様々なアルゴリズムが考えられていますが、代表的なものとして、遺伝的アルゴリズムがあります。名前のとおり、生物の遺伝や進化のように、遺伝子に相当するパラメータを交叉や突然変異などによって変更させながら、目的に合う適応度の高い固体を優先的に選択して、最適解を求める手法です。今回は、Platypusに搭載されているNSGA-Ⅱという遺伝的アルゴリズムを使って計算してみます。
円管の伝熱と圧力損失
円管の出口温度は、以下の方法で求めます。
また、直管の圧力損失は、以下の手法で計算します。
多目的最適化の結果
Platypusを使って多目的最適化を行った結果を示します。
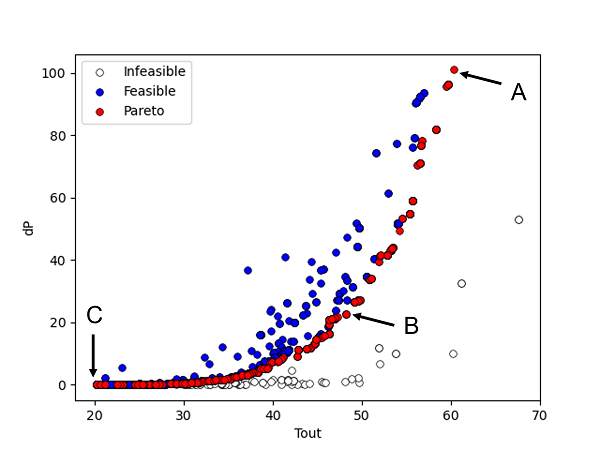
横軸に空気の出口温度、縦軸に圧力損失を取り、プロットした図です。赤点は最終の最適解、青点と白点は最適化の途中で得られた解を表します。青は制約条件を満たしており、白は制約条件を満たさない解です。
赤の最適解は、弓なりの曲線上に分布しています。これをパレート解と言います。今回目的関数が2つありましたが、出口温度を最大化しようとすれば、伝熱量を上げるため管の長さを長くしなければなりません。しかし、そうすると圧力損失が大きくなってしまい、圧力損失を最小化する目的が満たされなくなってしまいます。
このように、目的が複数ある場合、あちらを立てればこちらが立たずという、相反関係になる場合があります。このような関係をトレードオフの関係と言います。
多目的最適化でトレードオフの関係になると、解は一つに定まらず、このような曲線上(3次元では曲面上)に並びます。
図のA点の解は、管長さが6.0m、直径が0.10mを示しています。出口温度は60℃と最も高いですが、圧損も100Paと高い結果です。B点は、長さ4.6m、直径0.13mで、出口温度48℃、圧損23Paと中間的な解になっています。C解は、長さ0.12m、直径0.98mで、出口温度20℃、圧損4.0e-5Paと圧損が最も低い結果です。
では、実際にどれが最適解なのかは、このパレート解の中から、こちら側が選んでやる必要があります。C点は圧損は小さいが、出口温度が全く上昇しないので意味がないし、Aは圧損が高すぎて使えない、だとすると中間的なBを採用しようといった選択を行います。
相関分布
計算データを分析するのにデータの相関を見ることがあります。Pythonではseabornというライブラリを使うと簡単に図示することができます。
今回の最適化の結果データから、設計変数と目的関数の散布図をseabornでプロットすると以下のようになります。
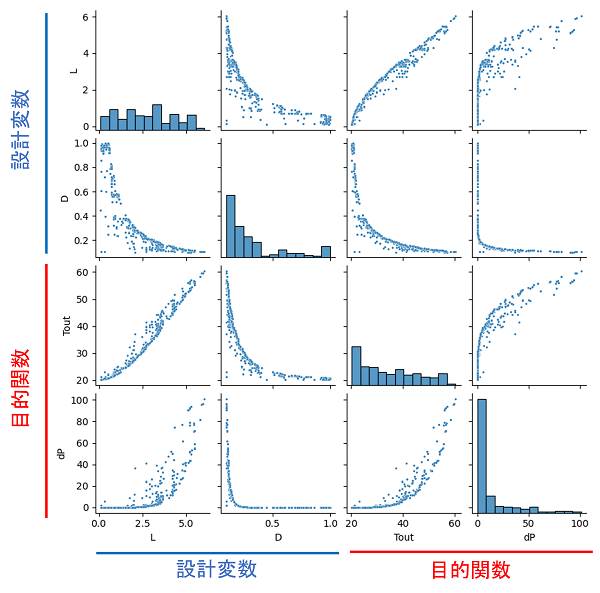
各変数どうしの散布図を描画できます。対角成分のグラフはその変数の頻度分布を示しています。各変数どうしがどのような関係にあるかが一目でわかります。例えば、管長さLと出口温度Toutの関係は、Lが大きくなると、Toutも大きくなっています。また、直径Dが大きくなると、Toutは小さくなっています。
これらの関係は相関係数をとることで、はっきり表すことができます。以下の図は、各変数の相関係数をとってコンターで図示したものです。相関係数は、pandasなどのライブラリで計算して、seabornで簡単に図示することができます。相関係数は1に近いと正の相関、-1に近いと負の相関を意味します。各変数がそれぞれどのような相関を持っているかも、数値的に確かめることができます。
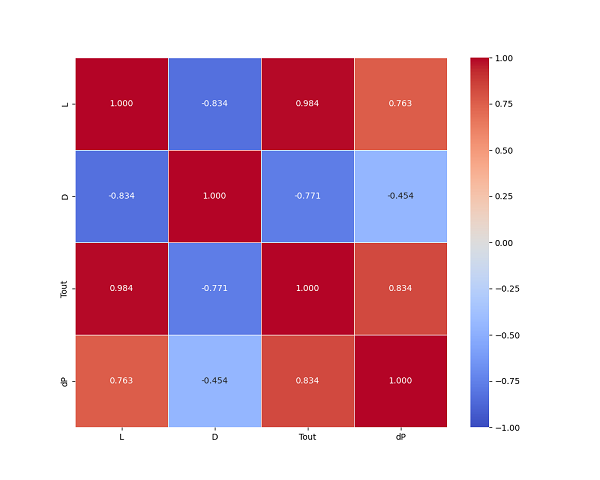
このようにPythonを使うと、製品設計に役立つ最適化を行うことができるので、ぜひトライしてみてください。