図形の体積・面積を計算する
球、円（円柱、円錐）、四角形（四角柱、四角錐）、三角形（三角柱、三角錐）の各図形の体積や面積を計算します。各図形の形状を入力すると、面積や体積が計算され出力されます。
球
球
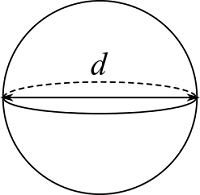
| 入力 | 直径 $d$ | |
|---|---|---|
| 結果 | 表面積 $S_s$ | |
| 体積 $V$ |
$$S_s = \pi d^2$$
$$V = \frac{\pi d^3}{6}$$
円、円柱、円錐
円
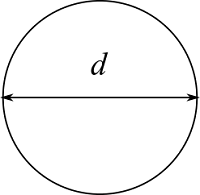
| 入力 | 直径 $d$ | |
|---|---|---|
| 結果 | 面積 $S$ |
$$S = \frac{\pi d^2}{4}$$
円柱、円錐
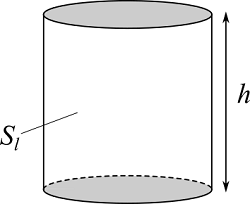
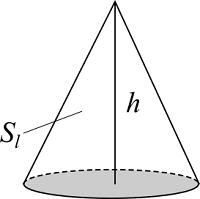
| 入力 | 高さ $h$ | |
|---|---|---|
| 円柱 | 側面積 $S_l$ | |
| 表面積 $S_s$ | ||
| 体積 $V$ | ||
| 円錐 | 側面積 $S_l$ | |
| 表面積 $S_s$ | ||
| 体積 $V$ |
円柱
$$S_l = \pi d h$$
$$S_s = S_l + 2 S$$
$$V = S h$$
円錐
$$S_l = \frac{\pi d}{2} \sqrt{ \frac{d^2}{4} + h^2}$$
$$S_s = S_l + S$$
$$V = \frac{1}{3}S h$$
※底面積$S$は、円の結果が使用されます。
四角形、四角柱、四角錐
四角形
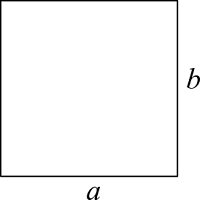
| 入力 | 辺長さ $a$ | |
|---|---|---|
| 辺長さ $b$ | ||
| 結果 | 面積 $S$ |
$$S = a b$$
四角柱、四角錐
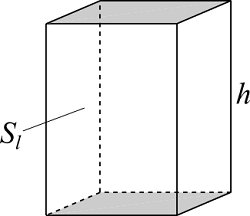
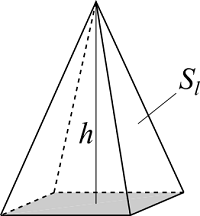
| 入力 | 高さ $h$ | |
|---|---|---|
| 四角柱 | 側面積 $S_l$ | |
| 表面積 $S_s$ | ||
| 体積 $V$ | ||
| 四角錐 | 側面積 $S_l$ | |
| 表面積 $S_s$ | ||
| 体積 $V$ |
四角柱
$$S_l = 2(a+b)h$$
$$S_s = S_l + 2S$$
$$V = S h$$
四角錐
$$S_l = a \sqrt{(\frac{b}{2})^2+h^2} + b \sqrt{(\frac{a}{2})^2+h^2}$$
$$S_s = S_l + S$$
$$V = \frac{1}{3} S h$$
※底面積$S$は、四角形の結果が使用されます。
三角形、三角柱、三角錐 ：底辺と高さより計算
三角形
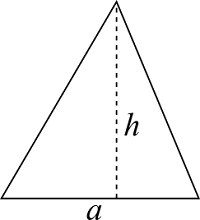
| 入力 | 底辺 $a$ | |
|---|---|---|
| 高さ $h$ | ||
| 結果 | 面積 $S$ |
$$S = \frac{1}{2} a h$$
三角柱、三角錐
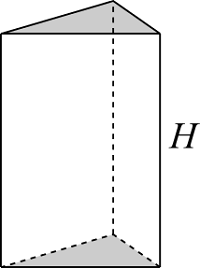
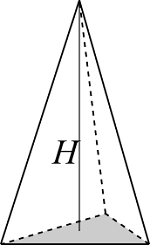
| 入力 | 高さ $H$ | |
|---|---|---|
| 三角柱 | 体積 $V$ | |
| 三角錐 | 体積 $V$ |
三角柱
$$V = S H$$
三角錐
$$V = \frac{1}{3} S H$$
※底面積$S$は、三角形の結果が使用されます。
三角形、三角柱、三角錐 ：三辺の長さより計算
三角形
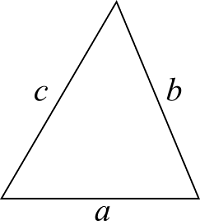
| 入力 | 辺長さ $a$ | |
|---|---|---|
| 辺長さ $b$ | ||
| 辺長さ $c$ | ||
| 結果 | 面積 $S$ |
ヘロンの公式より
$$S = \sqrt{s (s-a) (s-b) (s-c)}$$
$$s = \frac{a+b+c}{2}$$
三角柱
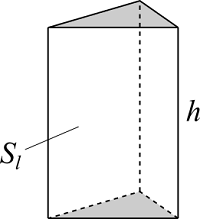
| 入力 | 高さ $h$ | |
|---|---|---|
| 三角柱 | 側面積 $S_l$ | |
| 表面積 $S_s$ | ||
| 体積 $V$ |
$$S_l = (a+b+c)h$$
$$S_s=S_l + 2S$$
$$V = S h$$
※底面積$S$は、三角形の結果が使用されます。
三角錐
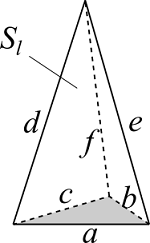
| 入力 | 辺長さ $d$ | |
|---|---|---|
| 辺長さ $e$ | ||
| 辺長さ $f$ | ||
| 三角錐 | 側面積 $S_l$ | |
| 表面積 $S_s$ | ||
| 体積 $V$ |
$$S_l = S_{dae} + S_{ebf} + S_{fcd}$$
$$S_s = S_l + S$$
$$\begin{split} V^2 = \frac{1}{144} &[d^2 b^2 (-d^2+e^2+f^2+a^2-b^2+c^2) \\ &+ e^2 c^2 (d^2-e^2+f^2+a^2+b^2-c^2) \\ &+ f^2 a^2 (d^2+e^2-f^2-a^2+b^2+c^2) \\ &- d^2 e^2 a^2 – e^2 f^2 b^2 -d^2 f^2 c^2 -a^2 b^2 c^2] \end{split}$$
※底面積$S$は、三角形の結果が使用されます。
関連項目
3次元座標での三角形の面積を計算します。三角形の面積は、ベクトル積から計算されます。点1から点2へ向かうベクトルと点1から点3へ向かうベクトルのベクトル積が、平行四辺形の面積を表すため、その半分が三角形の面積となります。