目次
開水路の等流計算(水深と勾配から流量を求める)
河川や水路などの開水路で、水深や流速が場所により変化しない流れを等流といいます。このページでは、Manning(マニング)公式を用いた等流の計算を行ないます。ここでは、水深と勾配から流量、フルード数を計算します。
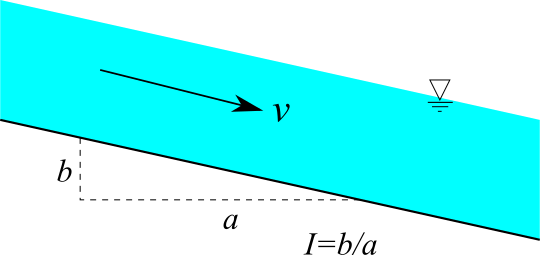
Manning公式
等流のManning公式は以下で表されます。
$$v = \frac{1}{n} R^{2/3} I^{1/2}$$
$v$:流速、$n$:マニングの粗度係数、$R$:径深($=A/S$)、$A$:水路断面積、$S$:潤辺、$I$:水路勾配
フルード数
フルード数 $Fr$ は、以下の式で計算されます。
$$Fr = \frac{v}{\sqrt{g D}}$$
$v$:流速、$g$:重力加速度、$D$:水理水深($=A/T$)、$A$:水路断面積、$T$:水面幅
計算
水路断面形状は、矩形、台形、円形のものを計算できます。
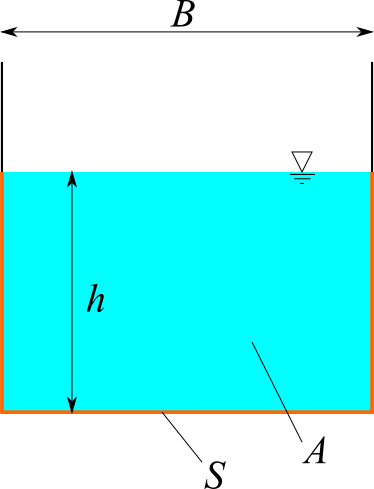
矩形
矩形断面の水路を計算します。水路勾配 $I$、マニング粗度係数 $n$、水深 $h$、水路幅 $B$ を入力してください。流速 $v$、流量 $Q$、フルード数 $Fr$ が計算されます。
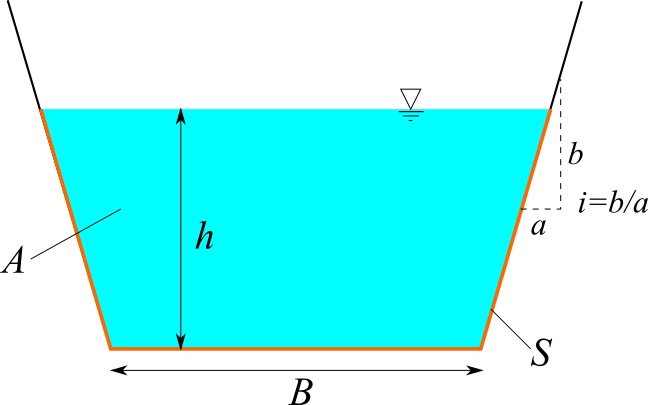
台形
台形断面の水路を計算します。水路勾配 $I$、マニング粗度係数 $n$、水深 $h$、水路底幅 $B$、法面勾配 $i$ を入力してください。流速 $v$、流量 $Q$、フルード数 $Fr$ が計算されます。
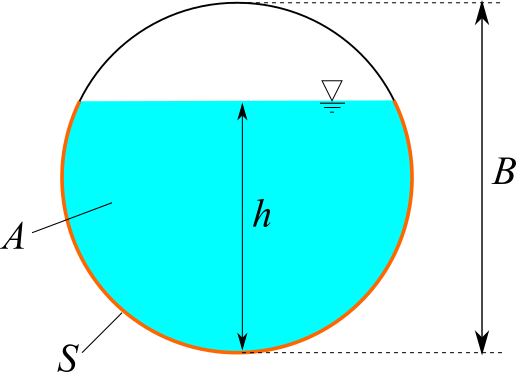
円形
円形断面の水路を計算します。水路勾配 $I$、マニング粗度係数 $n$、水深 $h$、水路直径 $B$ を入力してください。流速 $v$、流量 $Q$、フルード数 $Fr$ が計算されます。