目次
開水路の等流計算(流量と勾配から水深を求める)
河川や水路などの開水路で、水深や流速が場所により変化しない流れを等流といいます。このページでは、Manning(マニング)公式を用いた等流の計算を行ないます。ここでは、流量と勾配から水深、フルード数を計算します。
Manning公式
等流のManning公式は以下で表されます。
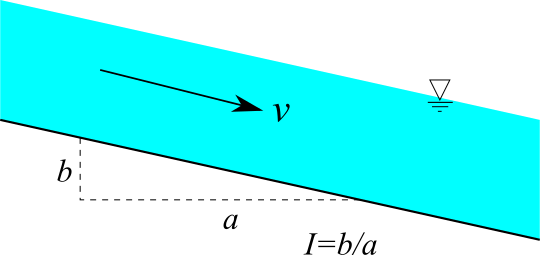
$$v = \frac{1}{n} R^{2/3} I^{1/2}$$
$v$:流速、$n$:マニングの粗度係数、$R$:径深($=A/S$)、$A$:水路断面積、$S$:潤辺、$I$:水路勾配
流量(流速)と勾配が与えられたとき、水深は代数的に求めるのが難しいため二分法により数値的に求めています。
フルード数
フルード数 $Fr$ は、以下の式で計算されます。
$$Fr = \frac{v}{\sqrt{g D}}$$
$v$:流速、$g$:重力加速度、$D$:水理水深($=A/T$)、$A$:水路断面積、$T$:水面幅
計算
水路断面形状は、矩形、台形、円形のものを計算できます。
※断面形状により流量(流速)の最大値が決まるものがあるため、大きな流量(流速)を与えると数値解が求まらない場合があります。その場合は、NaNを返します。
矩形
矩形断面の水路を計算します。流量 $Q$ または流速 $v$、水路勾配 $I$、マニング粗度係数 $n$、水路幅 $B$ を入力してください。水深 $h$、フルード数 $Fr$ が計算されます。
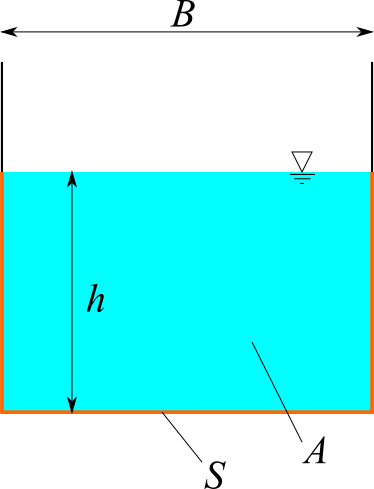
※矩形水路では、水深を大きくすると径深が $R=B/2$に漸近するため、流速もある値に漸近します。そのため、それより大きな流速では解が存在しません。この場合、NaNが表示されます。
台形
台形断面の水路を計算します。流量 $Q$ または流速 $v$、水路勾配 $I$、マニング粗度係数 $n$、水路底幅 $B$、法面勾配 $i$ を入力してください。水深 $h$、フルード数 $Fr$ が計算されます。
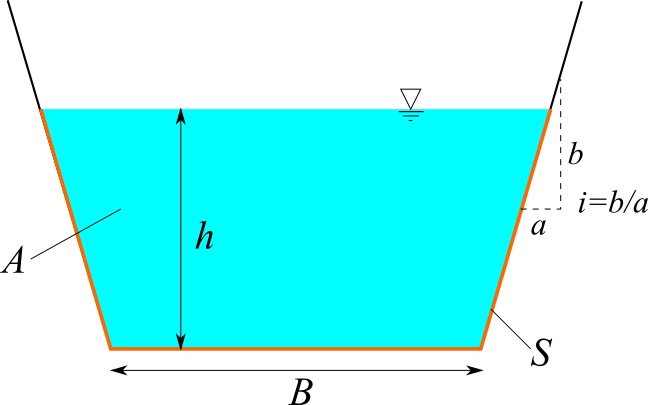
円形
円形断面の水路を計算します。流量 $Q$ または流速 $v$、水路勾配 $I$、マニング粗度係数 $n$、水路直径 $B$ を入力してください。水深 $h$、フルード数 $Fr$ が計算されます。
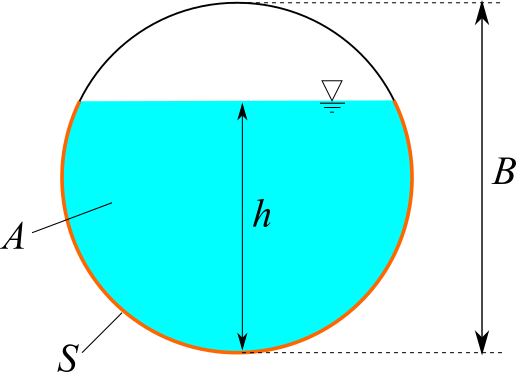
※円形水路では、$h/B = 0.93818$ のときに最大流量となります(最大速度は $h/B = 0.8128$ のとき)。満水時の流量と最大流量との間の流量では、解となる水深が数学的に2つ存在します。満水時の流量より小さい流量では水深の解は1つとなり、最大流量より大きな流量では解は存在しません。存在しない解に対しては、NaNが表示されます。
