「オンライン熱解析CATTHM」のための熱抵抗、熱容量を計算するページです。
目次
熱抵抗の計算
伝熱面積と各値を入力してください。熱抵抗が算出されます。合成熱抵抗は、算出されている熱抵抗について直列と並列で計算されます。値を入力しない箇所は熱抵抗は算出されません。
計算式
伝導による熱抵抗
物質の内部を熱伝導で熱が移動する場合の熱抵抗です。
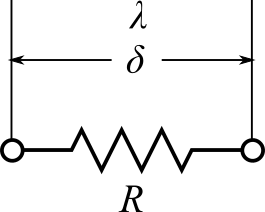
ノード間距離 $\delta$ で、熱伝導率 $\lambda$、伝熱面積 $A$ の伝導による熱抵抗 $R$ は、
$$R=\frac{\delta}{\lambda A}$$
で表されます。
対流による熱抵抗
固体表面から対流(自然対流、強制対流)により熱移動する場合は、熱伝達率を用いて熱抵抗を表すことができます。
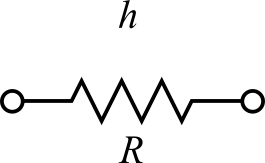
熱伝達率 $h$ 、伝熱面積 $A$ の対流による熱抵抗 $R$ は、
$$R=\frac{1}{h A}$$
となります。
熱伝達率 $h$は、自然対流の空気で 5 [W/(m2 K)]、強制対流の空気で 50 [W/(m2 K)]、自然対流の水で 500 [W/(m2 K)]、強制対流の空気で 5000 [W/(m2 K)] のオーダーです。ただし、流れの性状や流速により実際にはかなり幅があります。詳細は以下のページを参照ください。
放射による熱抵抗
2つのノード間の放射による熱移動量$Q$[W]は、ノードの温度を$T_i$[K]、$T_j$[K]とすると、次式で表されます。
$$Q=\sigma \varepsilon A (T_{j}^4-T_{i}^4)$$
ここで、$\sigma=5.67\times 10^{-8} $[W/(m2 K4)]:ボルツマン定数、$\varepsilon$:放射率(0~1)
これを変形すると、
$$Q=\sigma \varepsilon A (T_{j}^2+T_{i}^2) (T_{j}+T_{i}) (T_{j}-T_{i})$$
となります。したがって、放射による熱抵抗値は、以下のように書けます。
$$R=\frac{1}{\sigma \varepsilon A (T_{j}^2+T_{i}^2) (T_{j}+T_{i})}$$
この式には、各ノードの温度自体が含まれており事前に算出できないため、CATTHMではソルバー内部で計算時に求めています。ツールへの入力としては、以下の定義による放射係数を与えます。
$$放射係数=\varepsilon A$$
流体移動による熱抵抗
換気などで空気のような流体が通風する場合は、流体の持ち込みによる熱移動が起きます。
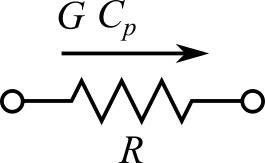
この時の熱移動量$Q$[W]は、以下のようになります。
$$Q=G C_p (T_{j}-T_{i})$$
ここで、$G$:流体の質量流量[kg/s]、$C_p$:流体の比熱[J/(kg K)]。
したがって、熱抵抗は、
$$R=\frac{1}{G C_p}$$
となります。
※配管のような流体が流れる流路を熱回路網法の定式化だけで解くことはできません。この熱抵抗モデルは、温度固定の外気ノードから室内のノードに通風するような場合に使用します。
※配管の流体ながれを考慮する場合は、流体抵抗網法の機能をご使用ください。
熱抵抗の合成
直列抵抗の場合
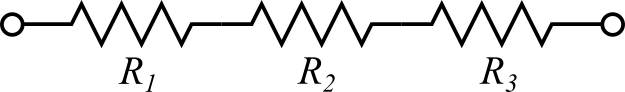
熱抵抗が直列に接続されている場合、合成熱抵抗は各熱抵抗の総和となり、
$$R=R_1+R_2+R_3$$
のように計算できます。
並列抵抗の場合
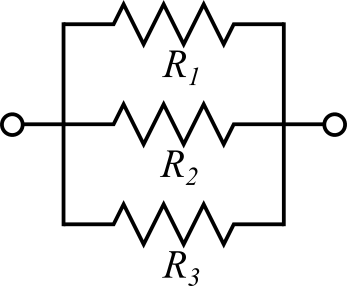
熱抵抗が並列に接続されている場合、合成熱抵抗は以下のように表されます。
$$\frac{1}{R}=\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$
熱容量の計算
密度、体積、比熱を入力すると熱容量が計算されます。
計算式
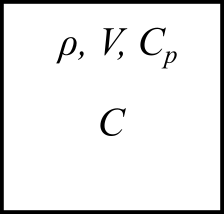
ノードの熱容量 $C$ は、密度 $\rho$、体積 $V$、比熱 $C_p$ より、
$$C=\rho V C_p$$
で計算できます。
