前回は有限体積法の計算のもとになる線形方程式を作成するPythonプログラムを作りました。
今回はその線形方程式を解くための解法について説明したいと思います。
目次
線形方程式系
これまで見てきたように、セル $C$ とその隣接セル $F$ に対して、線形方程式を書くと次のような式になります。
$$ a_C T_C + \sum_F a_F T_F = b_C \tag{8-1}$$
実際にはこの式がセル数分あり連立方程式を形成しています。このような線形方程式の連立方程式を線形方程式系(system of linear algebraic equations)といいます。
これらの式をセル数分書くのは大変なので、次のように表します。
$$ {\bf A} {\bf T} = {\bf b} \tag{8-2}$$
ここで、${\bf T}$ は各セルの温度 $T_C$ をセル数分格納したベクトルを表します。${\bf b}$ は同様に $b_C$ のベクトル量です。${\bf A}$ は係数 $a_C$、$a_F$ を表す行列で係数行列と呼びます。この式は次の図のような構造をしています。
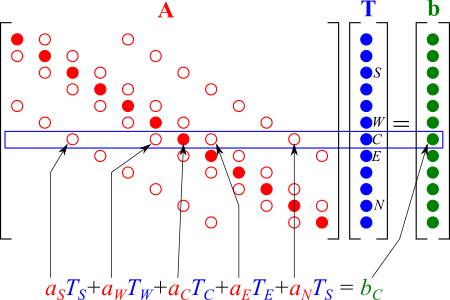
行列 ${\bf A}$ は ● がセル $C$ の係数 $a_C$ を表していて、行列の対角成分に位置しています。○ は隣接セルの係数 $a_F$ を表しています。この行列は対角成分を挟んで折り返すと係数が一致します。このような行列は対称行列(symmetric matrix)と呼ばれます。
また、●○以外の成分は全てゼロです。セルの数がいくら多くても、一つの行に高々5つの成分(自分自身と隣接セル4つ)しかなく、ほとんどがゼロになっています。このような行列を疎行列(sparse matrix)といいます。
線形方程式系の解法
(8-2)式の線形方程式系を解くと、求めたい温度の解が得られます。この解法には実に様々な方法があります。
差分法のときに紹介したヤコビ法やガウス=ザイデル法もその一つです。今回の問題もガウス=ザイデル法を使って解くことは可能です。$T_C=$ の式に変形して反復計算するだけなので、プログラムは簡単に作れます。ただし、実際にガウス=ザイデル法のプログラムで計算してみると、収束までの反復回数が多く、なかなか収束しないことがわかります。
そこで今回は、ガウス=ザイデル法と同じ反復解法の一つである共役勾配法(conjugate gradient method、CG法)で解いてみたいと思います。
共役勾配法とは対称正定値行列(※)を解くための反復解法の一種で、収束が早く今回のような大規模な疎行列が係数行列となる線形方程式系の解法としてよく使われます。共役勾配法にはいくつかの種類がありますが、汎用の流体解析ソフトなどでもこれらの解法が使われています。当サイトのCATCFDzeroはBiCGSTABという共役勾配法の一種を使っています。
今回はベースとなるオリジナルの共役勾配法で解いてみたいと思います。
※ 行列が正定値であるとは、対称行列 ${\bf A}$ が $0$ でない任意のベクトル ${\bf x}$ に対して $({\bf x}, {\bf A} {\bf x}) > 0$ を満たすことをいいます。。。ここではこれ以上深入りしないことにしましょう。
共役勾配法
共役勾配法のコンセプトは、次の式の最小値を求めるというものです。
$$f({\bf T}) = \frac{1}{2}( {\bf T}, {\bf A} {\bf T}) - ({\bf b}, {\bf T}) \tag{8-3}$$
ここで、$({\bf b}, {\bf T})$ はベクトル ${\bf b}$ と ${\bf T}$ の内積を表します 。
なぜこの最小値が(8-2)式を解くことになるのかというと、$f({\bf T}) $ の最小値のところでは $f({\bf T}) $ を ${\bf T}$ で微分した値(勾配)$f'({\bf T})$ がゼロになることに由来します。すなわち、
$$f'({\bf T}) = {\bf A} {\bf T} - {\bf b} = 0 \tag{8-4}$$
となります。これは(8-2)式を示しています。つまり、$f({\bf T})$ が最小になるときの ${\bf T}$ が、求める解となるわけです。
共役勾配法は反復法の一種です。反復法とは、適当な初期値から始めて、次のステップの解を近似しながら繰り返し計算を行い、目的とする解を求める方法です。
今、反復ステップ $k$ の温度を ${\bf T}_k$ とすると、次のステップの近似解を
$${\bf T}_{k+1} = {\bf T}_k + \alpha_k {\bf d}_k \tag{8-5}$$
として求めることにします。ここでベクトル ${\bf d}_k$ は次の解への方向ベクトルです。関数 $f({\bf T})$ の最小値(極値)を求める方法の一つは、次の図の青色の経路をたどる方法がイメージしやすいです。青色の経路は関数の負の勾配 $-f'({\bf T})$ に沿って進んでいく方法です。(図は関数 $f({\bf T})$ の等高線を表していて、その中央が最小値(ちょうどお椀の底)になっています。その最小点で真の解 ${\bf T}$ をとります。)
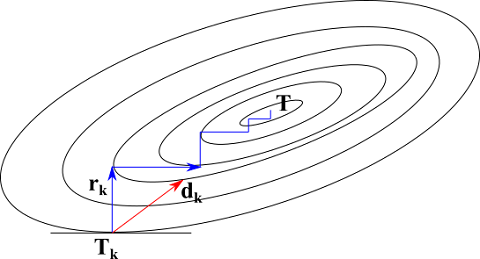
ここで ${\bf r}_k$ は残差ベクトルといいます。
$${\bf r}_k = {\bf b} - {\bf A} {\bf T}_k = -f'({\bf T}_k) \tag{8-6}$$
この方法は、最急降下法(steepest descent method)と呼ばれています。(8-5)式で ${\bf d}_k = {\bf r}_k$ とした場合です。勾配 ${\bf r}_k$ に沿って下っていき、その線上の最低点まできたら再びその地点での勾配方向に沿って下っていきます。ただし、この方法は図からもイメージできるように真の解 ${\bf T}$ にたどり着くまでに反復回数が多そうです。
実際の真の解 ${\bf T}$ の方向は図の赤いベクトルの方向であり、${\bf r}_k$ の方向から少しずれています。これを次式で求めることにします。
$${\bf d}_{k} = {\bf r}_{k} + \beta_{k-1} {\bf d}_{k-1} \tag{8-7}$$
これは前のステップの ${\bf d}_{k-1}$ を使って ${\bf r}_k$ から少しずらすことを意味します。このとき、${\bf d}_{k}$ と ${\bf A}{\bf d}_{k-1}$ が直交するように $\beta$ を選んでやります。このようにすると、これまでの方向と重ならない方向で経路を決めることができて効率的です。このベクトル ${\bf d}$ の方向を行列 ${\bf A}$ に対して共役な方向といいます。
この考え方から $\alpha$ と $\beta$ は次のように計算されます。
$$\alpha_k= \frac{({\bf d}_k, {\bf r}_k)}{({\bf d}_k, {\bf A}{\bf d}_k)} \tag{8-8}$$
$$\beta_k= \frac{({\bf r}_{k+1}, {\bf r}_{k+1})}{({\bf r}_k, {\bf r}_k)} \tag{8-9}$$
共役勾配法のアルゴリズム
数値計算をするために共役勾配法のアルゴリズムを整理しておきます。
- 適当な初期値 ${\bf T}_0$ を決める。
- ${\bf r}_0 = {\bf b} - {\bf A} {\bf T}_0$、 ${\bf d}_0 = {\bf r}_0$ とする。
- 収束するまで以下の計算を繰り返す。
① $\alpha_k=({\bf d}_k, {\bf r}_k)/({\bf d}_k, {\bf A}{\bf d}_k) $
② ${\bf T}_{k+1} = {\bf T}_k + \alpha_k {\bf d}_k$
③ ${\bf r}_{k+1} = {\bf r}_k - \alpha_k{\bf A} {\bf d}_k$
④ 残差 ${\bf r}_{k+1}$ で収束判定。収束なら終了。
⑤ $\beta_k= ({\bf r}_{k+1}, {\bf r}_{k+1})/({\bf r}_k, {\bf r}_k)$
⑥ ${\bf d}_{k+1} = {\bf r}_{k+1} + \beta_k {\bf d}_k $
共役勾配法の導出過程はややこしいですが、アルゴリズムはとてもシンプルです。
残差と収束判定
反復法はどこかで収束を判定し、計算を打ち切ってやる必要があります。以前、ガウス=ザイデル法では、前のステップとの差をとってそれが小さくなった段階で収束と判定しました。
$$ ||{\bf T}_{k+1} - {\bf T}_k|| \le \varepsilon \tag{8-10} $$
$|| {\bf x} ||$ はベクトル $ {\bf x} $ の絶対値(ノルム)を表します。これは誤差基準の収束判定です。
今回の共役勾配法では残差 ${\bf r}$ を計算しています。残差とは、(8-6)式を見ればわかるように、解くべき線形方程式系(8-2)式の右辺と左辺の差を表しています。残差がゼロになると、(8-2)式が満たされ真の解が求まったことになります。
この残差がゼロになる(実際には小さな数値 $\varepsilon$ 以下になる)のを収束判定に使います。残差を使う収束判定の式もいろいろありますが、今回は右辺 ${\bf b}$ の絶対値で割った相対残差という指標を使うことにします。
$$ \frac{||{\bf r}_{k+1}||}{||{\bf b}||} \le \varepsilon \tag{8-11}$$
(8-11)式を満たせば共役勾配法の反復を終了します。
まとめ
今回は解くべき線形方程式系を行列で表し、共役勾配法という解法について説明しました。共役勾配法は、数学的な話は難しいですが、プログラムにするためのアルゴリズムはとてもシンプルです。
次回は共役勾配法をPythonでプログラミングして、有限体積法のプログラムを完成させたいと思います。
