前回は陽解法のCFL条件と時間刻みのとり方について説明しました。
今回は時間刻みを大きくとることができる数値解法をご紹介します。
目次
陰解法
FTCS法は熱伝導方程式
$$\frac{\partial T}{\partial t} = \alpha \frac{\partial^2 T}{\partial x^2} \tag{1}$$
を時間に対して前進差分、空間に対して中心差分で離散化した解法でした。
では、$T_i^{n+1}$ について考えた時、時間に対して後退差分、空間に対して中心差分で離散化してみましょう。
$n+1$ の項は左辺に、$n$ の項は右辺に集めて整理すると、
となります。ここで $c = \alpha \Delta t/ \Delta x^2$。
FTCS法では現在の時刻 $n$ から次の時刻 $n+1$ が計算できましたが、(3)式は次の時刻 $n+1$ が左辺に複数あり単純に代入するだけでは求めることができません。このように時刻 $n+1$ の未知数が空間項にも含まれる解法を陰解法といいます。また、(2)式のように既知の時刻 $n$ の項が時間微分だけに現れるものを完全陰解法と呼びます。
連立方程式
では、(3)式のように未知数が複数ある式を解くにはどうすればよいのでしょうか?
実は中学校のとき、この解き方は習っているはずです。次の方程式は解けますか?
$$\left\{ \begin{aligned} 3x-2y+z &=3\\ 2x+3y-z &=1\\ x+3y-2z &=2\end{aligned} \right. \tag{4}$$
そうです。これは連立方程式です。答えは、$(x, y, z) = (1, -1, -2)$ です。係数を合わせて式どうしを足したり引いたりして計算すれば求まりますね。
(3)式もこれと同じです。空間に100個の点があるとすると、100個式ができます。この連立方程式を解いていけば時刻 $n+1$ の未知数が求まるというわけです。
連立方程式の数値計算法
3つの式であれば手で計算できますが、100個はとても無理です。では数値計算でコンピューターに計算させましょう。連立方程式を数値的に計算させる方法はたくさん考えられています。ここでは、よく使われる反復解法というのをご紹介します。反復解法は何か適当な値から始めて繰り返し計算をしていき、真の値に近づけるという方法です。
ヤコビ法
まずは一番簡単なヤコビ法(Jacobi Method)で(4)式を解いてみます。
(4)式の第1式を $x$ が左辺に、それ以外が右辺来るように変形します。
$$x = \frac{1}{3} ( 3+2y-z) \tag{5}$$
同じように第2式は $y$、第3式は $z$ が左辺に来るように変形します。
$$\left\{ \begin{aligned} x &= \frac{1}{3} ( 3+2y_*-z_*)\\ y &= \frac{1}{3} (1-2x_*+z_*)\\ z &= -\frac{1}{2}(2-x_*-3y_*)\end{aligned} \right. \tag{6}$$
ここで、右辺に持ってきた変数に * の印を付けています。
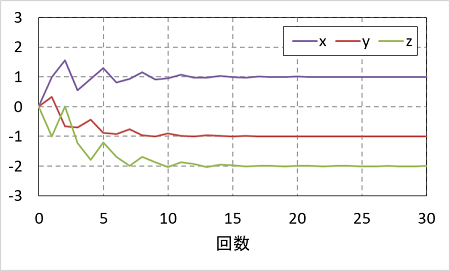
初期の値を適当に $(x_*, y_*, z_*) = (0,0,0)$ としましょう。これを(6)式の右辺に代入して計算すると、$(x, y, z) = (1, 0.3333, -1)$ となります。次にこれを再度右辺に代入して計算すると、$(x, y, z) = (1.5555,-0.6666,0)$となります。再度右辺に代入して。。。これを繰り返して行くと解 $(x, y, z) = (1, -1, -2)$ に近づいていきます。下のグラフは繰り返し回数に対する各変数の変化をプロットしたものです。
手計算だと大変なのでプログラムにしてみましょう。
eps = 1.0e-6
x = 0.0
y = 0.0
z = 0.0
for iter in range(100):
xp = x
yp = y
zp = z
x = 1.0 / 3.0 * (3.0 + 2.0 * yp - zp)
y = 1.0 / 3.0 * (1.0 - 2.0 * xp + zp)
z = -1.0 / 2.0 * (2.0 - xp - 3.0 * yp)
print("{0:3d} {1:15.9f} {2:15.9f} {3:15.9f}".format(iter, x, y, z))
resd = abs(x - xp) + abs(y - yp) + abs(z - zp)
if resd <= eps:
breakx、y、z に初期値 0.0 を入れて、forループで繰り返し計算をしています(この繰り返しをイタレーションと呼ぶことにします)。xp、yp、zpは一つ前のイタレーションの値が入ります。(6)式の * 付きがこれに相当します。
ここで、resd は前のイタレーションの値と新しく計算された値の差の絶対値 abs() を変数ごとに足したものです。そして、if文で eps 以下になると、break という命令を実行します。break はforループから抜けろという命令です。つまり、resd が eps 以下になると計算終了となります。
ここは何をしているかというと、反復解法は繰り返し計算なのでどこかで計算をやめてやる必要があります。もちろん、真の解と同じになったら止めればよいのですが、真の解がそもそもわかりません。上のグラフを見ると、計算で出てくる結果はある値に収束していって、徐々に変化がなくなっていることがわかります。つまり、前のイタレーションに対して変化が十分に小さくなったところで計算を止めるというのが一つの方法になります。
resd は前のイタレーションとの差をとっており、この値が十分小さく eps 以下になると計算を止めるという方法を採用しています。これを収束判定といいます。収束判定の方法は他にもいろいろ考えられています。また、eps を収束判定基準といいますが、どのくらいの値で計算を止めるべきかというのも問題によります。今は $10^{-6}$ という小さな値にしていますが、これくらいの差であればまあよしとしようということです。
今回の例では 63イタレーション(forループが0から始まるので実際には64回目)で収束と判定され計算終了となりました。そのときの結果は
でほぼ真の解になっています。
ガウス=ザイデル法
ヤコビ法と似た方法ですが、繰り返し回数が少なくてすむガウス=ザイデル法(Gauss-Seidel Method)というのがあります。
ヤコビ法では(6)式は前のイタレーションの結果を右辺に代入していきましたが、第1式の計算結果の $x$ を第2式を計算するときに右辺に代入する、また第2式の結果の $y$ の値を第3式の右辺に代入する、という具合に計算済みの値を使ってどんどん計算を進めていくのがガウス=ザイデル法です。
$$\left\{ \begin{aligned} x &= \frac{1}{3} ( 3+2y_*-z_*)\\ y &= \frac{1}{3} (1-2x+z_*)\\ z &= -\frac{1}{2}(2-x-3y)\end{aligned} \right. \tag{7}$$
プログラムは次のようになります。
eps = 1.0e-6
x = 0.0
y = 0.0
z = 0.0
for iter in range(100):
xp = x
yp = y
zp = z
x = 1.0 / 3.0 * (3.0 + 2.0 * y - z)
y = 1.0 / 3.0 * (1.0 - 2.0 * x + z)
z = -1.0 / 2.0 * (2.0 - x - 3.0 * y)
print("{0:3d} {1:15.9f} {2:15.9f} {3:15.9f}".format(iter, x, y, z))
resd = abs(x - xp) + abs(y - yp) + abs(z - zp)
if resd <= eps:
breakヤコビ法と違うのは xp、yp、zp の値を使わずに、計算済みの x、y、z をそのまま右辺に代入できるようにしているところです。これを計算してみるとわずか19イタレーションで収束することがわかります。
熱伝導方程式を陰解法で解く
このように反復解法はプログラミングが簡単なのでよく使われる方法です。今回解く熱伝導方程式の陰解法にも、このガウス=ザイデル法を使うことにします。
熱伝導方程式の完全陰解法をガウス=ザイデル法で解いてみましょう。
(3)式を $T_i^{n+1}$ について整理します。
これは(6)式や(7)式と同じ形です。$T_i^n$ は前の時間ステップの既知の値です。$T^{n+1}$ は未知数なので、何か適当な初期値(一番よいのは前の時間ステップの 値 $T^n$ です)から始めて繰り返し計算をしていけばよいのです。
では、以前作ったFTCS法のPythonプログラムを陰解法に書き換えてみてください。
まとめ
本日は陰解法と連立方程式を解くヤコビ法やガウス=ザイデル法といった反復解法について説明しました。今までのプログラミングの知識があれば陰解法のプログラムも作ることができるので、ぜひチャレンジしてみてください。
次回は陰解法のプログラミングと時間刻み、CFL条件がどのようになっているか見ていきたいと思います。
