前回は構造格子のメッシュ情報を求めるPythonプログラムを作りました。
今回は有限体積法の計算のもとになる線形方程式を作成するプログラムを作っていきたいと思います。
目次
線形方程式
以前4-4章で構造格子での離散化を行い(4-12)式を得ました。これは各セルの温度 $T$ の一次式の形をしています。このような式を線形方程式といいます。セル $C$ とその隣接セル $F$ に対して、一般的に書くと次のような式です。
$$ a_C T_C + \sum_F a_F T_F = b_C \tag{7-1}$$
そして、この式がセル数分あり、連立方程式を形成します。この連立方程式を解くと求めたい温度の解が求まるというわけです。
方程式をどう解くかというのは、また次回お話したいと思いますが、今回は係数 $a$ や $b_C$ を計算して解くべき線形方程式を作っておきましょう。
各係数 $a$ と $b_C$ は(4-13)式のように計算できます。もう一度書いておきます。
$$\begin{split} a_E &= -\lambda_e \frac{S_e}{d_{CE}} \\ a_W &= -\lambda_w \frac{S_w}{d_{CW}} \\ a_N &= -\lambda_n \frac{S_n}{d_{CN}} \\ a_S &= -\lambda_s \frac{S_s}{d_{CS}} \\ a_C &= - (a_E + a_W + a_N + a_S) \\ b_C &= q_C V_C \end{split} \tag{7-2} $$
境界面では少し式が違いますが、これは4-5章でお話したとおりです。面積 $S$ や 距離 $d$ は与えた形状データから求められますし、$b_C$ の項も既知の値から計算できます。
面での熱伝導率
では、$\lambda_e$ の値はどうすればよいでしょうか?これは面 $e$ での熱伝導率を表しています。熱伝導率がいたるところ同じであれば、一定値として与えればよいのですが、今回の問題では熱伝導率が場所によって異なっています。
単純に考えるとセル中心と面の位置から線形補間で求めるという方法がありますが、ここでは調和平均という方法を使って面での値を求めます。
$$\lambda_e = \frac{\lambda_C \lambda_E}{(1-g_e) \lambda_C + g_e \lambda_E} \tag{7-3}$$
ここで、$g_e = d_{Ce} / (d_{Ce} + d_{eE})$。
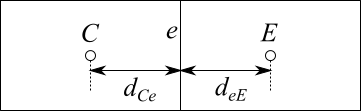
これは $C-e$ 間 と $e-E$ 間の総括的な熱伝達を考えると求まります。
Pythonプログラム
これで全ての量が求められるのでPythonでプログラムを作成していきます。線形方程式の係数を求めるプログラムを以下に示します。
以下、前回説明したところは端折って説明します。
import numpy as npまずnumpy配列を使うので、numpyをインポートしておきます。
#-- temperature
temp = np.full(ncell+1, 300.0)温度の配列 temp を作り、初期値を設定します。配列の要素番号はセル番号に対応させるため、1 からncell までとするので、ncell+1 個分の配列を作ります。これで、要素番号 0 から ncell までの配列ができます。要素番号 0 はダミーの要素としておきます。初期値は300Kとします。
#-- thermal conductivity
cond = np.full_like(temp, 100.0)
for i in range(1, nx+1):
for j in range(1, ny+1):
icell = i + (j - 1) * nx
x = (i - 0.5) * dx
y = (j - 0.5) * dy
if y >= 0.8:
cond[icell] = 10.0次に熱伝導率の配列 cond を作ります。full_like(temp, 100.0) は、temp と同じ要素数で100.0の値に設定するという意味です。ひとまず熱伝導率を一様に 100W/(mK)にしています。問題を忘れた方はもう一度見直しておいてください。
次に、forループで i、jを回し、y が0.8m以上のところで、熱伝導率を10W/(mK)に設定しています。
#-- heat source
qc = np.zeros_like(temp) qc はセルの発熱量 $q_C$ で、zeros_like(temp) は temp と同じ要素数で値をゼロにするという意味です。今回の問題では特に発熱量は与えないのでゼロとしています。
s = [dy, dy, dx, dx]
dcf = [dx, dx, dy, dy]
volume = dx * dy少し飛ばしてこの部分ですが、s は面の面積 $S$ を表す配列で、4つの面 $e$、$w$、$n$、$s$ の順番に面積を格納しています。dcf はセル $C$ の中心と隣接セル $F$ の中心との間の距離 $d_{CF}$ を表す配列で $E$、$W$、$N$、$S$ の順番に格納されています。 volume はセルの体積です。今は均一なサイズのセルを考えているので、どのセルでもこれらの値は変わりません。
ac = np.zeros_like(temp)
af = np.zeros((ncell+1, 4))
bc = np.zeros_like(temp)
cnbor = np.zeros_like(af, dtype='int')ここでは係数の配列を作っています。ac は係数 $a_C$、af は係数 $a_F$、bc は $b_C$ です。af は各セルに対して4つの隣接セル分必要なので、第一要素がセル番号、第二要素が4つの面のインデックスを表す2次元配列として定義しています。
cnbor はセルに隣接する4つのセル番号を格納しておくための配列です。これも、af と同じ2次元配列です。dtype='int' はその数値が整数であることを示しています。dtypeを指定しないと、デフォルトで浮動小数点数となっています。
ac[icell] = 0.0
bc[icell] = qc[icell] * volume次に i、j でforループを回します。まず、ac にゼロ、bc に $q_C V_C$ をセットします。
for iface in range(4):次に4つの面でループを回します。ftype と inbor は前回説明したとおり、面のタイプと隣接セルの番号を求めています。
#-- matrix
if ftype == 'internal': # internal face
gf = 0.5
condf = cond[icell] * cond[inbor] / ((1.0 - gf) * cond[icell] + gf * cond[inbor])
a_f = -condf * s[iface] / dcf[iface]
a_c = -a_f
b_c = 0.0ここは、面のタイプが 'internal' (境界面ではない内部の面)の場合、(7-2)式から係数を計算しています。
else: # boundary face
if ftype == 'right' and y <= 0.2:
a_f, a_c, b_c = boundary(icell, iface, 'dirichlet', tb=500.0)
elif ftype == 'top' and x <= 0.5:
a_f, a_c, b_c = boundary(icell, iface, 'dirichlet', tb=300.0)
elif ftype == 'left':
a_f, a_c, b_c = boundary(icell, iface, 'mixed', ta=400.0, ht=100.0)
else:
a_f, a_c, b_c = boundary(icell, iface, 'neumann', qb=0.0)ここは面タイプが境界面の場合、境界条件を適用する部分です。例えば、if ftype == 'right' and y <= 0.2: は、境界面が 'right' (右端面)でかつ y ≦ 0.2 の場合のディリクレ条件( $T_b = 500K$ )を与えます。ここでは、boundary() という関数で各係数を計算するようにしています。
boundary() の関数はforループに入る前に定義しています。
def boundary(icell, iface, btype, tb=300.0, qb=0.0, ta=300.0, ht=10.0):
condf = cond[icell]
dcb = 0.5 * dcf[iface]
if btype == 'dirichlet': # Dirichlet
a_b = -condf * s[iface] / dcb
a_f = 0.0
a_c = -a_b
b_c = -a_b * tb
elif btype == 'neumann': # Neumann
a_f = 0.0
a_c = 0.0
b_c = -qb * s[iface]
elif btype == 'mixed': # Mixed
htc = condf / dcb
htf = ht * htc / (ht + htc)
a_b = -htf * s[iface]
a_f = 0.0
a_c = -a_b
b_c = -a_b * ta
return a_f, a_c, b_c 関数の引数は、セル番号 icell、面インデックス iface、境界タイプ btype、ディリクレ境界の温度 tb、ノイマン境界の熱流束 qb、混合境界の外部温度 ta、熱伝達率 ht です。
tb=300.0 としているのは、呼び出し側で tb を指定しない場合、デフォルトとして 300.0K が使用されるということを意味します。
指定された境界タイプに応じて、各係数が計算されます。ディリクレ条件は(5-3)式、ノイマン条件は(5-6)式、混合条件は(5-13)式のとおりです。そして各係数を返します。
ac[icell] += a_c
af[icell][iface] = a_f
bc[icell] += b_c 面のforループの説明に戻ります。ループの最後で、ac、af、bc に各面の係数をセットします。ac と bc は各面からの寄与を足し合わせています。
プログラムでは最後 print で計算された係数を出力しています。値を確認してみてください。
まとめ
今回は線形方程式の各係数を計算するプログラムを作成しました。この係数が分かればあとは線形方程式を解いていくだけです。次回は線形方程式を解く方法について説明していきます。
