前回は有限体積法の離散化についてお話しました。
今回は境界条件の離散化について考えてみたいと思います。
目次
境界条件の種類
前回行った離散化は、領域の内部でセル $C$ が4つのセル $E$、$W$、$N$、$S$ に接しているときのものでした。では、領域の端の境界に接しているセルではどのように離散化すればよいでしょうか。境界条件には様々な種類がありますが、今回の問題では3つのタイプの境界条件について考えます。
- ディリクレ(Dirichlet)境界条件
境界面の値を固定する境界条件。温度を直接指定する。 - ノイマン(Neumann)境界条件
境界面の勾配を固定する境界条件。熱流束を指定する。断熱は熱流束ゼロのノイマン条件に相当。 - 混合(Mixed)境界条件
1と2の混合型の境界条件(Robin条件ともいう)。外部温度と熱伝達率が指定されている条件に相当。
ではひとつずつ見ていきましょう。
ディリクレ(Dirichlet)境界条件
ディリクレ境界は境界面での温度を固定する境界条件です。今、セル $C$ の面 $e$ が境界面だとします。境界面の温度を $T_b$ とします。セル $E$ は領域の外なので存在していません。

この場合、前回の(4-8)式はどうなるかというと、
となります。$x$ の微分はセル $C$ と面 $e$ の値を用いて差分をとっています。$d_{Ce}$ はセル $C$ の中心から面 $e$ までの距離(すなわち $\Delta x / 2$)です。$T_b$ は条件として与えるので既知の値です。
その他の面は前回と同じなので、境界セル $C$ についての式は次のように書けます。
セル $E$ がないので、$a_E$ はゼロとおきます。また、$a_e T_b$ は既知の項なので右辺に持ってきて、$q_C V_C$ と合わせて $b_C$ としています。
これがディリクレ境界面を持つセルの式になります。
ノイマン(Neumann)境界条件
ノイマン境界は境界面の熱流束を固定する境界条件です。断熱は熱流束ゼロのノイマン条件に相当します。
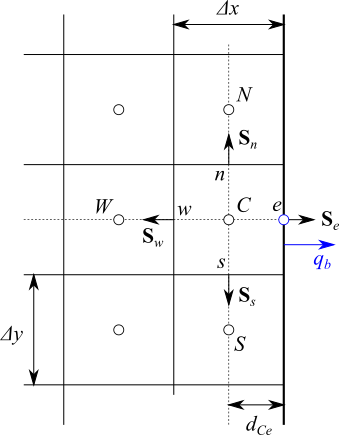
境界面の熱流束 $(-\lambda \nabla T)_e$ を $q_b$とすると次式が得られます。
$$(-\lambda \nabla T)_e \cdot {\bf S}_e = q_b S_e \tag{5-4}$$
これを同様にセル $C$ に適用すると、
$q_b S_e$ も既知の量なので、左辺に持ってきて $b_C$ の中に入れています。
この式では熱流束 $q_b$ はセルから流出する(熱が奪われる)ときに正($q_b>0$)となり、流入(熱が入ってくる)ときに負の値($q_b<0$)となります。また、式から明らかなように、断熱($q_b = 0$)であれば境界面 $e$ からの寄与は全くなくなることがわかります。
混合(Mixed)境界条件
ディリクレ条件とノイマン条件の混合型の境界条件を混合境界条件(またはRobin条件)といいます。熱伝導問題では外部温度と熱伝達率が指定されている条件に相当します。
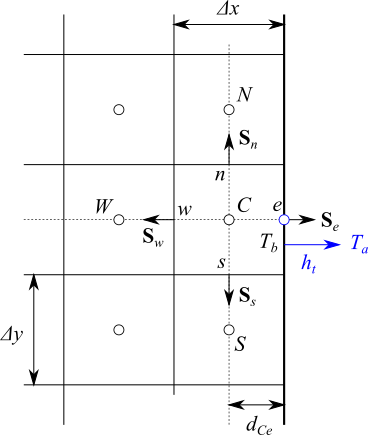
いま、境界面温度を $T_b$、外部温度を $T_a$、熱伝達率を $h_t$ とすると、外部への熱流束は $h_t ( T_b - T_a)$ と書けます。ノイマン条件と同じように表すと次のようになります。
一方で境界温度 $T_b$ を持つディリクレ条件と考えると(5-1)式になるので、2つを合わせると、
となり、これから $T_b$ は、
と求まります。(5-9)式を再度(5-7)式に代入して整理すると次式を得ます。
ここで、
$$H_e = \frac{ h_t (\lambda_e / d_{Ce})}{ h_t + (\lambda_e / d_{Ce})} \tag{5-11}$$
これも同様にセル $C$ について周りのセルの値を用いて表すと、
この場合も既知の項は左辺の $b_C$ に入れています。なお、$H_e$ はセル中心から外部までの総括的な熱伝達率に相当します。
このようにディリクレ条件とノイマン条件を合わせた形で混合条件の式を導くことができます。
まとめ
今回は3つの境界条件について考えましたが、どれも似たような式になりました。左辺は周りのセルの温度を用いて表され、右辺は条件として与える既知の量で求まります。
ここまでで、定常熱伝導方程式の有限体積法での式がだいたい導けました。細部が少し残っていますが、式ばかり出てきて頭が痛くなってきたと思いますので、次回はPythonでプログラミングを始めながら残りの部分をお話していくことにします。
