前回は熱伝導方程式のFTCS法によるPythonプログラムを作り計算してみました。
計算はできましたが、計算ステップ数が結構多くなっているので、時間刻みを大きくとって計算にかかる時間を節約したいですね。
時間刻みを変えてみる
今回のような1次元の問題では、計算もすぐに終わるのでそれほど気にはなりませんが、2次元や3次元の問題を解く場合、計算時間は急激に増大します。今の1次元の分割点数は 101 なので、2次元方向にも同じ点数とるとすると、単純計算では100倍計算時間が増えます。3次元だとさらにその100倍時間がかかることになります。1次元で数十秒で終わる計算も、3次元だと数十時間かかってしまうことになるわけです。
では、時間刻みを大きくとって計算終了までにかかるステップ数を減らしたらよいのではないでしょうか。今の設定では dt = 0.1 としています。これを5倍にして、dt = 0.5 としてみましょう。プログラムを変更し計算を実行してみてください。
結果の出力を見るととてもおかしなことになっています。
n: 200, time: 100.0, temp: -173503102124.873627
n: 400, time: 200.0, temp: -192787713995807071436926618669636229529600.000000
n: 600, time: 300.0, temp: -14860375061811717096221894594010699652792488166528499430302288969728.000000100秒のときの右端の温度はマイナスのとても大きな数値になっていて、その後も以上な数値が出力されています。その後、
RuntimeWarning: overflow encountered in double_scalars
...
n: 2600, time: 1300.0, temp: nan
n: 2800, time: 1400.0, temp: nanのようなメッセージが出力され、値が nan になっています。これは計算している数値が大きくなりすぎて計算できず、値が求まらない状態を示しています。このような状態を計算が発散するといいます。
CFL条件
なぜこのような状況になってしまったのでしょうか。実はFTCS法のような陽解法の数値計算法では時間刻みのとり方にある制約があります。熱伝導方程式の場合、時間刻み $\Delta t$ は次の条件を満たす必要があります。
$$\Delta t \leq \frac{\Delta x^2}{2 \alpha} \tag{1}$$
ここで $\alpha$ は熱拡散率。つまり時間刻み $\Delta t$ は$\Delta x^2/(2 \alpha)$ より小さくなければなりません。もし$\Delta t$ が大きいと上記のように計算が発散してしまいます。このような条件をCFL条件(Courant-Friedrichs-Lewy Condition)と呼んでいます。
今回の条件($\Delta x = 0.01$、$\alpha= 0.0001161$ )からCFL条件を計算すると、$\Delta t \leq 0.4306 $ である必要があります。この条件はかなり厳格で、今回の問題だと dt = 0.43 ではうまく計算できますが、dt = 0.44 では発散してしまいます。計算が発散せず安定に解くためにはCFL条件を満たす必要があるのです。
CFL条件は安定性解析という手法により導き出されるのですが、かなり数学的な話なのでここでは触れないことにします。その代わり、イメージで理解しておきましょう。FTCS法では次の時間の値 $T_i^{n+1}$ は、前の時間の値 $T_i^n$ とその両隣の値 $T_{i-1}^n$、$T_{i+1}^n$ を使って計算できることを示しました。つまり、$T_i^n$ の熱の情報は次の時間には $T_{i}^{n+1}$ と $T_{i-1}^{n+1}$、$T_{i+1}^{n+1}$ の3点に伝わることになります。下の図で青の矢印が計算によって伝わる熱を示しています。
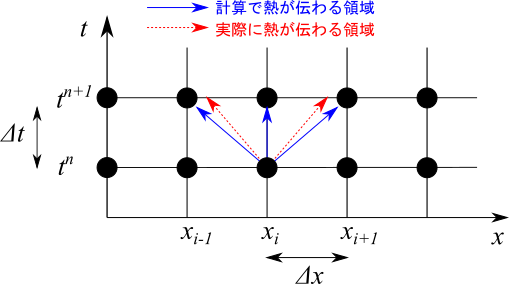
一方で実際に熱の伝わる速さは熱拡散率 $\alpha$ によって決まります。$\alpha$ が大きいと短い時間で遠くまで熱が伝わります。図の赤の矢印が実際に伝わる熱を示しています。この図は時間刻み $\Delta t$ が小さい場合のイメージです。計算で熱が伝わる領域より、実際に熱が伝わる領域の方が小さいです。
では、$\Delta t$ を大きくした場合はどうなるでしょうか。
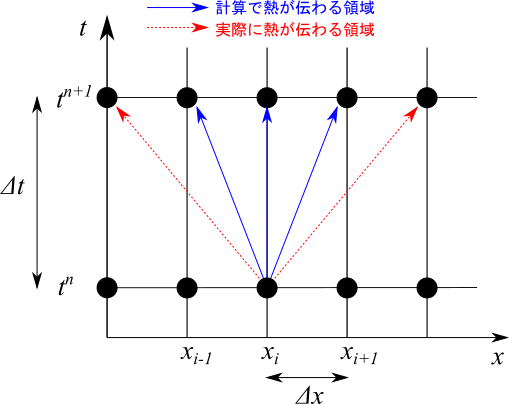
$\Delta t$ が大きいと、実際には熱はより遠くまで伝わります。しかし、計算ではその両隣の点までしか伝わりません。このように本来であれば遠くの点まで熱が伝わるのに、計算では影響範囲が限られてしまい矛盾が起きてしまいます。
つまり「計算で情報が伝わる速さ」は「実際に物理量が伝わる速さ」より大きくなっている必要があります。これがCFL条件です。
現在の時刻の情報から次の時刻を計算する陽解法では、このように時間刻みに対して厳しい制約があります。$\Delta t$ を大きくするためには、$\Delta x$ を大きくするしかありません。しかしそうすると、空間の解像度が悪くなり分布を的確に捉えることができなくなります。また逆に言えば、空間の解像度を上げるため $\Delta x$ を小さくしていくと、急激に $\Delta t$ を小さくする必要があります。
では計算期間が長い問題はどうしようもないのでしょうか?
実はこれを解決してくれる計算方法が考えられています。
話が長くなってきたので、今日はこの辺で終わりにしましょう。次回はこの数値計算法を紹介したいと思います。
まとめ
今回は時間刻みのとり方とCFL条件について説明しました。
次回は時間刻みを大きくとれる計算方法をご紹介いたします。
