前回は計算モデルを整理しました。これでプログラミングの準備が整いました。
今回から本当にプログラミングに入ります。
目次
熱伝導方程式のFTCS法プログラム
早速ですが、熱伝導方程式をFTCS法で解くPythonプログラムを載せておきましょう。
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
# input parameter
den = 8880.0
cp = 386.0
cond = 398.0
temp_bc = 100.0
temp_init = 0.0
lx = 1.0
nx = 101
tend = 20000.0
dt = 0.1
tout = 100.0
alpha = cond / (den * cp)
dx = lx / (nx - 1)
nt = int(tend / dt)
nout = int(tout / dt)
#initial condition
temp = np.full(nx, temp_init)
time = 0.0
temp_new = np.zeros(nx)
# Boundary condition
temp[0] = temp_bc # Dirichlet @ x=0
temp[nx-1] = temp[nx-2] # Neumann @ x=Lx
# graph data array
ims = []
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
gx = np.zeros(nx)
for i in range(nx):
gx[i] = i * dx
# time loop
for n in range(1, nt+1):
# FTCS
for i in range(1, nx-1):
temp_new[i] = temp[i] + dt * alpha * (temp[i+1] - 2.0 * temp[i] + temp[i-1]) / (dx * dx)
# update
for i in range(1, nx-1):
temp[i] = temp_new[i]
# Boundary condition
temp[0] = temp_bc # Dirichlet @ x=0
temp[nx-1] = temp[nx-2] # Neumann @ x=Lx
time += dt
if n % nout == 0:
print('n: {0:7d}, time: {1:8.1f}, temp: {2:10.6f}'.format(n, time, temp[nx-1]))
im_line = ax.plot(gx, temp, 'b')
im_time = ax.text(0, 110, 'Time = {0:8.1f} [s]'.format(time))
ims.append(im_line + [im_time])
# graph plot
ax.set_xlabel('x [m]')
ax.set_ylabel('Temperature [C]')
ax.grid()
anm = animation.ArtistAnimation(fig, ims, interval=50)
anm.save('animation.gif', writer='pillow')
plt.show()プログラムの説明
プログラムの内容を説明していきます。
ライブラリのインポート
まずはお決まりのライブラリのインポートです。
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as npグラフやアニメ作成ための matplotlib と、数値演算用に numpy をインポートします。
パラメータの入力
次に計算条件となるパラメータを入力していきます。
# input parameter
den = 8880.0
cp = 386.0
cond = 398.0
temp_bc = 100.0
temp_init = 0.0
lx = 1.0
nx = 101
tend = 20000.0
dt = 0.1
tout = 100.0密度 den、比熱 cp、熱伝導率 cond、温度固定の境界条件 temp_bc、温度の初期値 temp_init、棒の長さ lx、空間分割点数 nx、計算期間 tend、時間刻み dt、結果出力の時間間隔 tout を入力します。
alpha = cond / (den * cp)
dx = lx / (nx - 1)
nt = int(tend / dt)
nout = int(tout / dt)ここは入力した値から必要な他のパラメータを計算します。
alpha は熱拡散率、dx は空間分割の幅です。
nt は時間のステップ数を計算しています。int() は整数化するという関数です。tend も dt も小数点以下のある値です。これを浮動小数点数といいます。浮動小数点数を演算すると結果は浮動小数点数になるのですが、nt はステップ数なので整数として扱う必要があります。そこで、int() という関数で浮動小数点数を整数に変換しています(*)。
nout は結果出力のステップ間隔を計算しています。
* 通常プログラムでは変数が整数なのか浮動小数点数なのかを指定する必要があります。これを型の宣言といいますが、Pythonでは明示的に型を宣言しません。他のプログラム言語では、
int nt;
float dt;
のように int をつけると整数、float をつけると浮動小数点数というように、その変数がどのような型を示すのか明示的に宣言するものもあります。Pythonでは浮動小数点数には実際に小数点をつけて入力し、整数には小数点をつけずに入力することでPythonが自動的に型を判別しています。
nt = 100 →整数
dt = 0.1 →浮動小数点数
このプログラムでは、わかりやすくするため整数ではない浮動小数点数には、あえて
cp = 386.0
のように .0 をつけて入力しています。
初期条件の設定
次に初期条件を設定します。
#initial condition
temp = np.full(nx, temp_init)
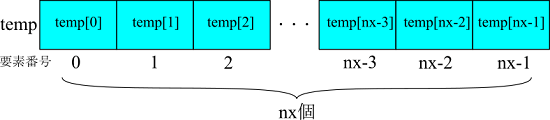
time = 0.0temp は離散化した各点の温度が入る配列です。前回示したように、番号 0番から nx-1 番までの要素を持つ配列として定義します。
np.full(nx, temp_init) は、nx個の要素を持つ配列を作り、その値を全て temp_init とするという関数です。これで、nx個全ての要素で初期値 temp_init の温度を持つ配列データが作られます。Pythonでは配列は要素番号0番から始まります。したがって、nx個の大きさの配列であれば、要素番号0番からnx-1番の番号がついています。
time は時間ですね。初期は 0.0秒からはじまります。
temp_new = np.zeros(nx)temp_new は後で出てきますが、温度の結果を一時的に格納するための配列です。np.zeros(nx) は大きさが nx個の配列を作り、その値を全て 0.0 にするという関数です。
境界条件の設定
次に境界条件を設定します。
# Boundary condition
temp[0] = temp_bc # Dirichlet @ x=0
temp[nx-1] = temp[nx-2] # Neumann @ x=Lx温度の配列の 0番目はディリクレ条件、逆の端 nx-1 番はノイマン条件です。
グラフ表示用のオブジェクト設定
次にグラフ表示用のオブジェクトを設定します。
# graph data array
ims = []
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)これは以前(地球の軌道シミュレーション)でやりましたね。
gx = np.zeros(nx)
for i in range(nx):
gx[i] = i * dxここは計算モデルの空間座標を gx という配列に入れています。後でグラフを描くのに使います。
gx = np.zeros(nx) で nx個の大きさの配列(値が 0.0)を作ります。その後、forループを回して要素の値を計算して入れていきます。i * dx で i 番目の要素の座標を計算して代入しています。gx[i] は i 番目の配列の要素を表します。
時間のループ
# time loop
for n in range(1, nt+1):ここから時間のループで、FTCS法の主要部分です。お馴染みforループですが、少しだけ今までと変えています。
時間の繰り返し回数は nt 回です。n はステップ数で1ずつ増分していきます。n in range(1, nt+1) は n を1からnt+1 まで増やしていくという命令です。ただし、nt+1 は含まれないので、一つ少ない nt までとなります。数学的に書くと、
$$ 1 \leqq n < nt+1 $$
です。結局、nt 回forループが繰り返され、n は1から nt まで1つずつ増分されます。n を1からはじめた方が結果出力のタイミングがわかりやすいので、今回はこのようにしています。
# FTCS
for i in range(1, nx-1):
temp_new[i] = temp[i] + dt * alpha * (temp[i+1] - 2.0 * temp[i] + temp[i-1]) / (dx * dx)さて、ここがFTCS法の計算部分です。forループで、番号1から nx-2 までループを回しています。このループは空間の要素に対するループです。range()は前述のとおりなので、要素番号に注意してください。要素番号0と nx-1 は一番両端の要素ですが、これは除外しています。この要素は境界条件で指定されるため、ここでは計算から外しているのです。
temp_new は先ほど配列を定義しておきましたが、計算結果を一時的に格納しておくための配列です。これまでは、
temp[i] = temp[i] + dt * alpha * (temp[i+1] - 2.0 * temp[i] + temp[i-1]) / (dx * dx)
のように、temp の値を直接更新する書き方をしていました。ところが、今回の計算ではこれではまずいです。今回は右辺は全て一つ前の時間のデータで計算しなくてはなりません。ところが、上記のように値を更新してしまうと、更新されたデータが次の要素の計算のときに右辺に入力されるため、おかしなことになってしまいます。これを避けるため別の配列に格納しているのです。
# update
for i in range(1, nx-1):
temp[i] = temp_new[i]FTCS法のforループが終わると、先程格納した temp_new を temp の配列にコピーして temp を更新します。ここではforループを回し temp_new の各要素を temp の同じ番号の要素に代入しています(*)。
* 以前配列を直接代入する処理をしたことがありました。そのとき、注意が必要と言いましたが、今回同じやり方を行うと問題が起きるため使っていません。もちろんうまく処理することはできますが、ここではあえて使わないことにします。Pythonでは配列の処理に対してさまざまな関数や方法が用意されています。しかし、ここではそのような方法は使わず、forループで要素ごとに処理をするというオーソドックスな方法で行っています。数値計算の初歩では、まずは要素ごとにどのような処理がされるか理解しておいた方がよいと思います。Python独自の処理方法はまた別の機会にご紹介します。
# Boundary condition
temp[0] = temp_bc # Dirichlet @ x=0
temp[nx-1] = temp[nx-2] # Neumann @ x=Lx
time += dt次に境界条件を適用します。0番と nx-1 番の一番端の要素に対して、ディリクレ条件とノイマン条件を設定しています。
時間 time は時間刻み dt だけ増分します。
if n % nout == 0:
print('n: {0:7d}, time: {1:8.1f}, temp: {2:10.6f}'.format(n, time, temp[nx-1]))
im_line = ax.plot(gx, temp, 'b')
im_time = ax.text(0, 110, 'Time = {0:8.1f} [s]'.format(time))
ims.append(im_line + [im_time])ここは前に出てきたのと同じです。画面への出力とアニメーションのコマを格納しています。今回は横軸に座標、縦軸に温度をプロットして、時間をグラフ上部に出力しています。
# graph plot
ax.set_xlabel('x [m]')
ax.set_ylabel('Temperature [C]')
ax.grid()
anm = animation.ArtistAnimation(fig, ims, interval=50)
anm.save('animation.gif', writer='pillow')
plt.show()ここも以前のとおりです。アニメーションの作成と、画面への出力を行います。
計算結果
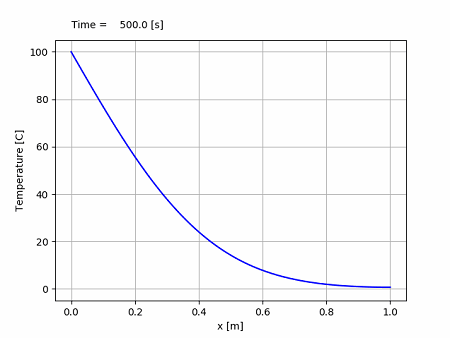
ではプログラムをPythonで実行してみてください。次のようなアニメーションが出力できましたか?
左端を100℃に熱しています。徐々に熱が伝わって左端から温度が上昇していきます。右端も徐々に温度が高くなっていきます。右端が50℃になるのに、1時間近くかかります。90℃になるには2.5時間ほどかかっています。意外と時間がかかることがわかります。
まとめ
今回は熱伝導方程式をFTCS法で計算するPythonプログラムを作りました。全体的な流れはこれまでと同様なのでそれほど難しくはないと思います。新しく、空間分布を持つ量に対して配列のループを回して計算していく、というのが加わりました。空間を差分法で解くプログラムはよく出てきますので、このような書き方は覚えておいてください。
ところで、今回の条件では熱が伝わるのに結構時間がかかりましたね。計算ステップ数も結構な数必要です。時間刻みをもう少し大きくとって計算回数を減らしたら良さそうですが。。。次回は時間刻みのとり方について触れてみたいと思います。
