Cantera：リチウムイオン電池の電気化学反応を計算する

2022/7/13 cantera

※Canteraバージョン：2.6.0

Canteraを使ってリチウムイオン電池の電気化学反応を計算してみる。

Canteraのホームページに例題が乗っているが、やや冗長なので要点をピックアップする。

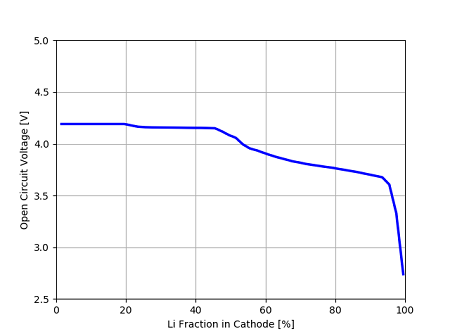
ここでは、電気化学反応を計算することで、アノード、カソードのリチウム濃度に対する開放電圧（Open Circuit Voltage）を求める。

参考文献：
Mayur, M.; DeCaluwe, S. C.; Kee, B. L.; Bessler, W. G. Modeling and simulation of the thermodynamics of lithium-ion battery intercalation materials in the open-source software Cantera. Electrochimica Acta, 2019, vol. 323, 134797.

計算モデル

アノードにグラファイト、カソードにLiCoO2を用いたリチウムイオン電池を考える。

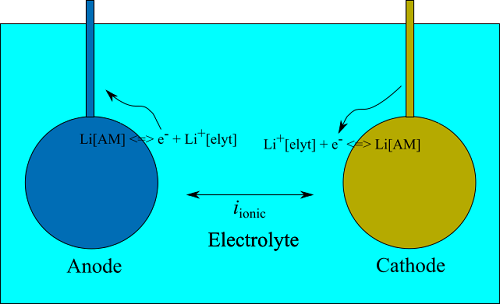
電極表面では、以下の電気化学反応が起こっている。

$$ \mathrm{Li^+[elyt]} + \mathrm{e^-[elde]} + \mathrm{V[AM]} \leftrightarrow \mathrm{Li[AM]} $$

ここで、elyt：電解質、elde：電極、AM：アノードまたはカソード、$ \mathrm{Li^+ }$：リチウムイオン、$ \mathrm{e^- }$：電子、$ \mathrm{V }$：空孔。

今回の計算では簡単のために、アノードとカソードのリチウム濃度が完全にバランスしていると仮定している。アノードのリチウム濃度を $x$ とすると、カソードのリチウム濃度は $1-x$ となる。

電位

ここで、電池の中の電位を考えると、次の４つの電位が関係してくる。

$\phi_{\mathrm{an}}$：アノードの電位
$\phi_{\mathrm{elyte, an}}$： アノード表面での電解質の電位
$\phi_{\mathrm{elyte, ca}}$： カソード表面での電解質の電位
$\phi_{\mathrm{ca}}$： カソードの電位

電池を流れる電流が保存するとすると、各電極表面のファラデー電流 $i_{\mathrm{Far}}$ と電解質を流れる電流 $i_{\mathrm{ionic}}$ が次のように等しくなる電位を求めることになる。

$$ i_{\mathrm{Far, an}} = i_{\mathrm{ionic}} = i_{\mathrm{Far, ca}} = i_{\mathrm{app}}$$

ここで、$i_{\mathrm{app}}$ は 系を流れる電流（ユーザー定義）。この例では開放電圧を求めるので、 $i_{\mathrm{app}}=0$ とする。

ファラデー電流とイオン電流

ファラデー電流の計算は、Bulter-Volmerの式を使う。

$$i = S_{\mathrm{elde}} i_0 \left[ \exp \left( \frac{F \beta \eta}{RT} \right) - \exp \left( - \frac{F (1 - \beta) \eta}{RT} \right) \right ]$$

ここで、$S_{\mathrm{elde}}$：電極の表面積、$i_0$：交換電流密度、$F$：ファラデー定数、$\beta$：電荷移動係数、$R$：気体定数、$T$：温度である。$\eta$ は過電圧で、

$$\eta = \Delta \phi - \Delta \phi_{eq}$$

$\Delta \phi = \phi_{\mathrm{elde}} - \phi_{ \mathrm{ elyte}}$ 、$ \Delta \phi_{eq} $ は平衡電位差である。

電解質中を流れるイオン電流は、抵抗を $R_{\mathrm{io}}$ とすると、

$$ i_{\mathrm{ionic}} = \frac{ \phi_{ \mathrm{elyte, ca}} - \phi_{ \mathrm{elyte, an}}}{ R_{\mathrm{io}} }$$

となり、電解質のカソード表面での電位は、

$$\phi_{\mathrm{elyte, ca}} = \phi_{ \mathrm{elyte, an}} + R_{\mathrm{io}} i_{\mathrm{ionic}} $$

となる。今は $ i_{\mathrm{ionic}}=i_{\mathrm{app}}=0$ であり、両電極表面での電位は等しい。

計算手順

数値計算の手順をまとめると以下のようになる。

  1. 電位の基準をアノード電位 $\phi_{\mathrm{an}}=0$ とする。アノードでのリチウム濃度を与え、電流が $i_{\mathrm{app}}$ となるような、電解質のアノード表面での電位 $ \phi_{ \mathrm{elyte, an}} $ を求める。
  2. $i_{\mathrm{app}}$ と $ \phi_{ \mathrm{elyte, an}} $ から、 電解質のカソード表面での電位 $\phi_{\mathrm{elyte, ca}} $ を求める。
  3. カソードでのリチウム濃度と $\phi_{\mathrm{elyte, ca}} $ を与え、 電流が $i_{\mathrm{app}}$ となるような、 カソードの電位 $ \phi_{ \mathrm{ca}} $ を求める。

Canteraのバージョン

電気化学計算をするためには、2.5.0a2以上のバージョンが必要となる。

反応メカニズムファイル

Canteraのインストールフォルダに反応メカニズムファイルlithium_ion_battery.yaml（旧バージョンではCTIファイル）が入っている。

アノードanode、カソードcathodeが、binary-solution-tabulatedというテーブル入力による新しい方法で定義されている。

thermo: binary-solution-tabulated

他に、電解質electrolyte、電極の導体electronが定義されている。

反応式は、前述の電気化学反応式がアノード、カソード表面について定義されている。

edge_anode_electrolyte-reactions:
- equation: Li+[elyt] + V[anode] + electron <=> Li[anode]  # Reaction 1
  id: anode_reaction
  rate-constant: {A: 2.028e+04, b: 0.0, Ea: 20.0 kJ/mol}
  exchange-current-density-formulation: true
  beta: 0.5

edge_cathode_electrolyte-reactions:
- equation: Li+[elyt] + V[cathode] + electron <=> Li[cathode]  # Reaction 2
  id: cathode_reaction
  rate-constant: {A: 5.629e+11, b: 0.0, Ea: 58.0 kJ/mol}
  exchange-current-density-formulation: true
  beta: 0.5

計算コード内容

ソースコード（GitHub）

import cantera as ct
print('Runnning Cantera version: ' + ct.__version__)

import numpy as np
from scipy.optimize import fsolve
import matplotlib.pyplot as plt

Pythonモジュールをインポートする。確認のためCanteraのバージョンを出力している。

scipy.optimizeは、Pythonの科学技術計算用ライブラリSciPyの最適化アルゴリズムであり、その中でfsolveは方程式の解を求めるためのモジュールである。ここでは、電流から電位を求めるのに使われる。

# define object
input_file = 'lithium_ion_battery.yaml'
anode = ct.Solution(input_file, 'anode')
cathode = ct.Solution(input_file, 'cathode')
elde = ct.Solution(input_file, 'electron')
elyte = ct.Solution(input_file, 'electrolyte')
anode_interface = ct.Interface(input_file, 'edge_anode_electrolyte', [anode, elde, elyte])
cathode_interface = ct.Interface(input_file, 'edge_cathode_electrolyte', [cathode, elde, elyte])

まず各オブジェクトを定義する。CTIファイルは上述のlithium_ion_battery.ctiを指定する。anode：アノード、cathode： カソード 、elde： 電極 、elyte： 電解質 、anode_interface： アノード表面 、cathode_interface：カソード表面を定義する。

# lithium mole fractions
X_Li_an = np.arange(0.005, 0.995, 0.02)
X_Li_ca = 1. - X_Li_an

アノードのリチウム濃度X_Li_anを0.005から0.995まで0.02刻みで設定する。この変数は配列となる。カソードのリチウム濃度は、1 - X_Li_anとして設定する。

# I_app = 0: Open circuit current
I_app = 0.

# At zero current, electrolyte resistance is irrelevant:
R_elyte = 0.

開放電圧を求めるため、電池を流れる電流 I_app をゼロに設定する。電解質の電気抵抗R_elyteを設定する（電流がゼロなので値は関係ない）。

# Temperature and pressure
T = 300 # [K]
P = ct.one_atm # [Pa]
F = ct.faraday # Faraday's constant
S_ca = 1.1167 # [m2] Cathode total active material surface area
S_an = 0.7824 # [m2] Anode total active material surface area
phases = [anode, elde, elyte, cathode, anode_interface, cathode_interface]
for ph in phases:
    ph.TP = T, P

T：温度、P：圧力、F：ファラデー定数、 S_ca：カソード面積、S_an：アノード面積を入力する。最後に各オブジェクトに設定する。

# function of anode current difference
def anode_curr(phi_l,I_app,phi_s,X_Li_an):
    # Set the active material mole fraction
    anode.X = 'Li[anode]:' + str(X_Li_an) + ', V[anode]:' + str(1 - X_Li_an)

    # Set the electrode and electrolyte potential
    elde.electric_potential = phi_s
    elyte.electric_potential = phi_l

    # Get the net product rate of electrons in the anode (per m2 interface)
    r_elec = anode_interface.get_net_production_rates(elde)

    anCurr = r_elec*ct.faraday*S_an
    diff = I_app + anCurr
    
    return diff

アノードの電流を計算する関数を定義する。電解質の電位phi_l、電流I_app、電極の電圧phi_s、電極のLi濃度X_Li_anを入力すると、アノード表面での電流とI_appとの差を計算して返す関数である。この関数を使うことにより、与えた電流 I_app との差がゼロになるような電解質電位phi_lを求める。

# function of cathode current difference
def cathode_curr(phi_s,I_app,phi_l,X_Li_ca):
    # Set the active material mole fractions
    cathode.X = 'Li[cathode]:' + str(X_Li_ca) + ', V[cathode]:' + str(1 - X_Li_ca)

    # Set the electrode and electrolyte potential
    elde.electric_potential = phi_s
    elyte.electric_potential = phi_l
    
    # Get the net product rate of electrons in the cathode (per m2 interface)
    r_elec = cathode_interface.get_net_production_rates(elde)
    
    caCurr = r_elec*ct.faraday*S_an
    diff = I_app - caCurr
    
    return diff

カソードについても同様の関数を準備する。

# solve
E_cell_kin = np.zeros_like(X_Li_ca)
for i,X_an in enumerate(X_Li_an):
    #Set anode electrode potential to 0:
    phi_s_an = 0
    E_init = 3.0
   
    # electrolyte potential at anode interface
    phi_l_an = fsolve(anode_curr,E_init,args=(I_app, phi_s_an, X_an))
    
    # electrolyte potential at cathode interface
    phi_l_ca = phi_l_an + I_app*R_elyte
    
    # cathode electrode potential
    phi_s_ca = fsolve(cathode_curr,E_init,args=(I_app, phi_l_ca, X_Li_ca[i]))
    
    # Calculate cell voltage
    E_cell_kin[i] = phi_s_ca - phi_s_an

計算を実行する。E_cell_kinは開放電圧が入る変数である。forループで、アノードのLi濃度（0.005～0.995）を変化させて計算する。

まず、基準となるアノードの電位phi_s_anをゼロに設定する。次に電解質のアノード表面での電位phi_l_anを計算する。計算はfsolveを使い、与えた電流I_app、アノード電位phi_s_an, Li濃度X_anに対して関数anode_currがゼロになるような電位を求めている。

次に、phi_l_anからカソード表面での電解質電位phi_l_caを求める。さらに、fsolveを用いカソードの電位phi_s_caを逆算して求める。

最終的に、カソードとアノードの電位差が開放電圧となる。

# plot
plt.plot(100*X_Li_ca, E_cell_kin, color='b', linewidth=2.5)
plt.xlabel('Li Fraction in Cathode [%]')
plt.ylabel('Open Circuit Voltage [V]')
plt.xlim(0, 100)
plt.ylim(2.5, 5)
plt.grid(True)
plt.show()

最後に、カソードのリチウム濃度に対する開放電圧をグラフにプロットする。

スポンサーリンク
科学技術計算のご相談は「キャットテックラボ」へ

科学技術計算やCAEに関するご相談、計算用プログラムの開発などお困りのことは「株式会社キャットテックラボ」へお問い合わせください。

お問い合わせはこちら

シェアする

フォローする

スポンサーリンク