開水路の限界水深と限界勾配

開水路の限界水深と限界勾配の計算

河川や水路などの開水路における、限界水深と限界勾配を計算します。ここでは、流量から限界水深と限界勾配を求めます。

比エネルギーと限界水深

開水路流れにおいて、全エネルギー水頭 $H$ は以下の式で表されます。

$$H = \frac{v^2}{2 g} + h + z_0$$

$v$：流速、$g$：重力加速度、$h$：水深、$z_0$：基準面から水路床までの高さ

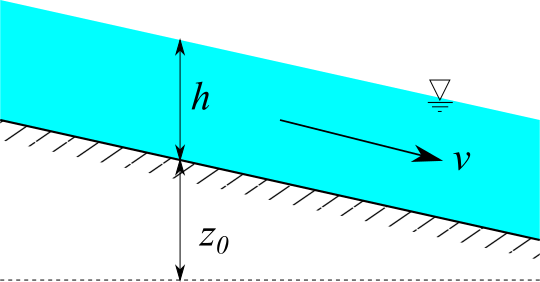
ここで、水路床高さ $z_0$ を基準にした水頭 $E$ を比エネルギーといいます。

$$E = H - z_0 = \frac{v^2}{2 g} + h$$

Aを水路断面積とすると、流量 は $Q = v A$ なので、

$$E = \frac{Q^2}{2 g A^2} + h$$

となります。

比エネルギー $E$ と水深 $h$ の関係は比エネルギー曲線といい下図のようになります。

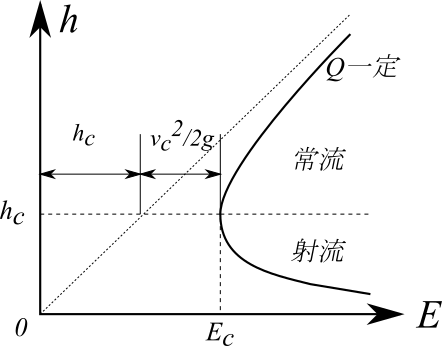
ある流量 $Q$ において比エネルギー $E$ が最小となる水深を限界水深 $h_c$ といいます。比エネルギーが $E_c$ 以下になるとその流量の水を流すことができなくなります。逆に言えば、ある比エネルギー $E$ に対して最大流量となる水深が限界水深 $hc$ となります。 

水深が限界水深となる流れ（$h=h_c$）を限界流、水深が限界水深より大きな流れ（$h>h_c$）を常流、限界水深より小さな流れ（$h<h_c$）を射流と呼びます。

常流は流れに与えられた変化が上流にも伝わります。一方、射流は上流には伝わらず下流のみに伝播します。

フルード数

フルード数 $Fr$ は、以下の式で計算されます。

$$Fr = \frac{v}{\sqrt{g D}}$$

$v$：流速、$g$：重力加速度、$D$：水理水深（$=A/T$）、$A$：水路断面積、$T$：水面幅

フルード数を用いて流れを整理すると、限界水深の限界流では $Fr = 1$ となります。常流では $Fr<1$、射流では $Fr>1$ となります。

流れの状態	水深	フルード数
常流	$h > h_c$	$Fr < 1$
限界流	$h = h_c$	$Fr = 1$
射流	$h < h_c$	$Fr > 1$

限界速度と限界勾配

限界水深のときの流速は限界流速 $v_c$ と呼ばれます。

また、等流水深 $h_0$ が限界水深と等しくなるとき（$h_0=h_c$）の水路勾配を限界勾配 $I_c$ といいます。水路勾配が限界勾配より小さい（$I<I_c$）と緩勾配水路となり等流水深は限界水深より大きく（$h_0>h_c$）なります。また、限界勾配より大きい（$I>I_c$）と急勾配水路となり等流水深は限界水深より小さく（$h_0<h_c$）なります。

	勾配	水深
緩勾配	$I<I_c$	$h_0 > h_c$
限界勾配	$I=I_c$	$h_0 = h_c$
急勾配	$I>I_c$	$h_0< h_c$

ここでは、等流のManning公式から勾配を計算しています。

$$v = \frac{1}{n} R^{2/3} I^{1/2}$$

$v$：流速、$n$：マニングの粗度係数、$R$：径深（$=A/S$）、$A$：水路断面積、$S$：潤辺、$I$：水路勾配

水路勾配 $I$ について整理すると、

$$I = \left( \frac{n v}{R^{2/3}} \right)^2$$

となり、この式で限界流速 $v_c$ と限界水深 $h_c$ を与えると限界勾配 $I_c$ が求まります。

計算

矩形、台形、円形の水路断面形状に対して、限界水深、限界流速、限界勾配を計算できます。与えられた流量と断面形状から限界水深を求めますが、限界水深は形状によっては代数的に求めるのが難しいため、比エネルギー $E$ が最小となる水深を $dE / dh = 0$ の式を数値的に解くことにより求めています。

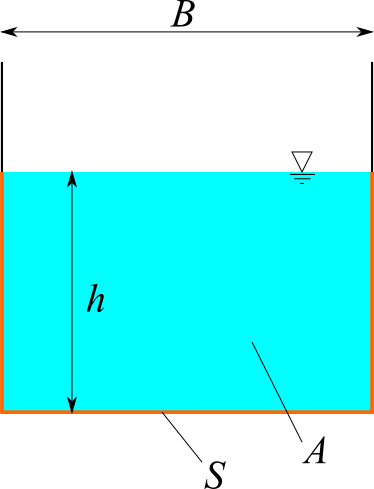
矩形

矩形断面の水路を計算します。流量 $Q$、マニング粗度係数 $n$、水路幅 $B$ を入力してください。限界水深 $h_c$、限界流速 $v_c$、限界勾配 $I_c$、フルード数 $Fr$ が計算されます。フルード数は、$Fr=1$となります。

流量 $Q$ [m3/s]
マニング粗度係数 $n$
水路幅 $B$ [m]

限界水深 $h_c$ [m]
限界流速 $v_c$ [m/s]
限界勾配 $I_c$
フルード数 $Fr$

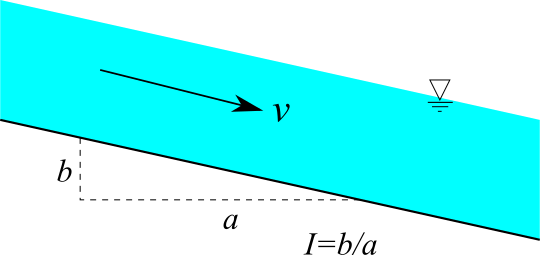
台形

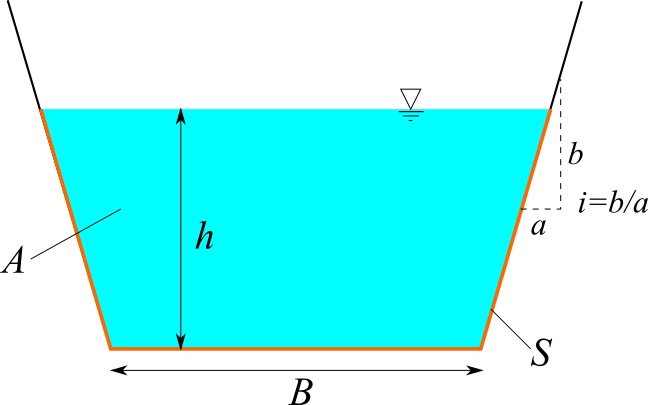
台形断面の水路を計算します。流量 $Q$、マニング粗度係数 $n$、水路底幅 $B$、法面勾配 $i$ を入力してください。限界水深 $h_c$、限界流速 $v_c$、限界勾配 $I_c$、フルード数 $Fr$ が計算されます。フルード数は、$Fr=1$となります。

流量 $Q$ [m3/s]
マニング粗度係数 $n$
水路幅 $B$ [m]
法面勾配 $i$

限界水深 $h_c$ [m]
限界流速 $v_c$ [m/s]
限界勾配 $I_c$
フルード数 $Fr$

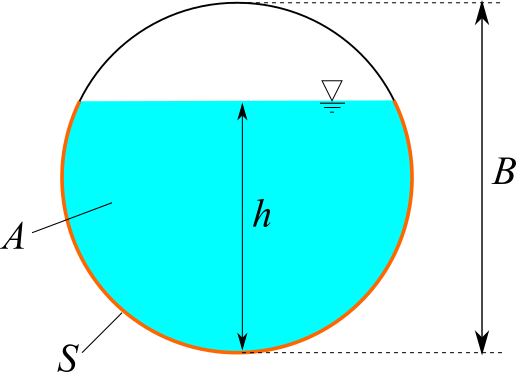
円形

円形断面の水路を計算します。流量 $Q$、マニング粗度係数 $n$、水路直径 $B$ を入力してください。限界水深 $h_c$、限界流速 $v_c$、限界勾配 $I_c$、フルード数 $Fr$ が計算されます。フルード数は、$Fr=1$となります。

流量 $Q$ [m3/s]
マニング粗度係数 $n$
水路直径 $B$ [m]

限界水深 $h_c$ [m]
限界流速 $v_c$ [m/s]
限界勾配 $I_c$
フルード数 $Fr$

関連項目

開水路の等流計算（流量を求める）
開水路の等流計算（水路勾配を求める）
開水路の等流計算（水深を求める）