Rohsenowの式による沸騰熱伝達の計算
沸騰による熱伝達は工業や身の回りの生活に欠かせない重要な現象です。沸騰は、沸騰が起こる壁面の表面過熱度$\Delta T$(表面温度$T_s$と飽和温度$T_{sat}$との差)により整理できます。下の図は、水の沸騰における表面過熱度に対する熱流束のグラフです(沸騰曲線)。
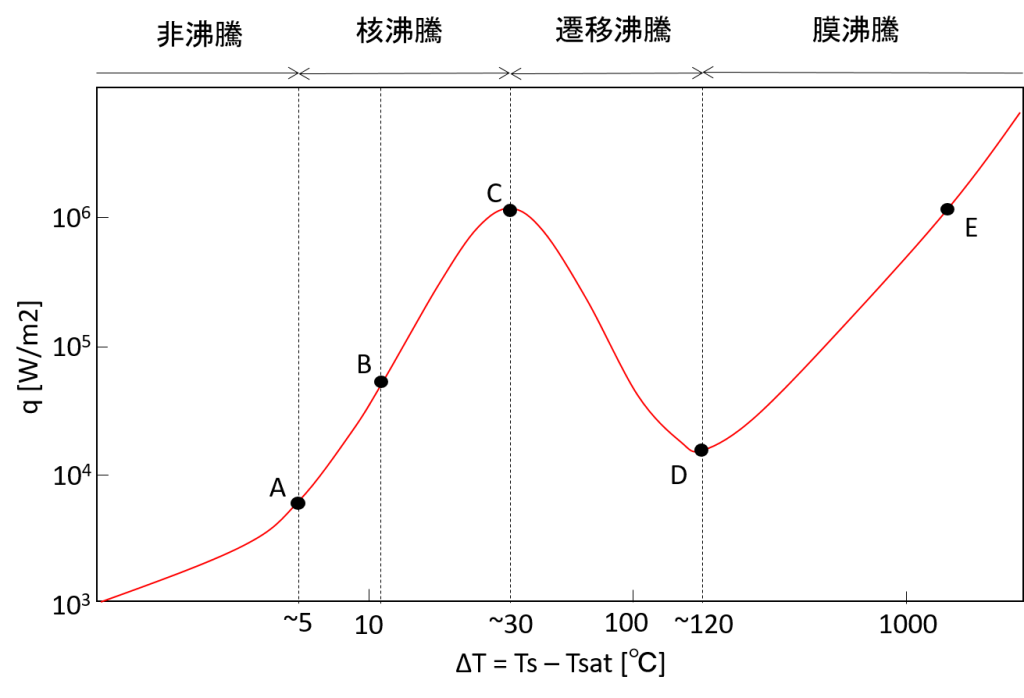
・非沸騰 (Non-boiling)
過熱度が小さいうちは、沸騰は起こらず自然対流により伝熱します。
・核沸騰 (Nucleate boiling)
沸騰開始点Aを超えると、沸騰が起こります。最初の内は、沸騰により発生した気泡は伝熱面を離れると消滅して、水面まで到達しません(サブクール沸騰、~B点)。さらに温度を上げていくと、気泡は途中で消滅せず水面まで到達するようになり、はげしく沸騰が起こります(飽和沸騰)。
・遷移沸騰 (Transition boiling)
熱流束が最大(C点)となったあと、熱流束はいったん減少します。これは、加熱表面が蒸気の膜で覆われて行くため、伝熱量が減少するためです。
・膜沸騰 (Film boiling)
熱流束はD点で極小となり(ライデンフロスト点)、その後また上昇します。この領域を膜沸騰と言い、加熱表面は蒸気の膜で完全に覆われた状態となっています。液体と加熱表面は接触が無く、輻射と伝導により伝熱が起こります。
Rohsenowの式
ここでは、Rohsenowの式を用いて核沸騰による熱流束を求めます。
$$q = \mu_l h_{fg} \left[ \frac{g \left( \rho_l - \rho_v \right)}{\sigma} \right]^\frac{1}{2} \left[ \frac{C_{pl} \left( T_s - T_{sat} \right)}{C_{sf} h_{fg} Pr_l^n} \right]^3 $$
$q$:沸騰熱流束[W/m2]、$\mu_l$:液体の粘度[Pa s]、$h_{fg}$:蒸発潜熱[J/kg]、$g$:重力加速度[m/s2]、$\rho_l $:液体密度[kg/m3]、$\rho_v$:蒸気密度[kg/m3]、$\sigma$:表面張力[N/m]、$C_{pl}$:液体の比熱[J/kg K]、$T_s$:加熱表面温度[℃]、$T_{sat}$:飽和温度[℃]、$C_{sf}$:表面係数、$Pr$:液体のプラントル数、$n$:係数
参考文献: Rohsenow, W. M. A Method of Correlating Heat Transfer Data for Surface Boiling of Liquids. Trans. ASME. 1952, vol. 74, p. 969–976.
表面係数と加熱面の表面温度を入力してください。水の沸騰熱流束が計算されます。伝熱表面を選択すると表面係数が反映されます。
※物性値は水で、以下の値で計算しています。
$\mu_l = 279 \times 10^{-6}$ [Pa s]、$h_{fg}=2257\times 10^3$ [J/kg]、$\rho_l = 957.9$ [kg/m3]、$\rho_v = 0.5955$ [kg/m3]、$\sigma = 58.9 \times 10^{-3}$ [N/m]、$C_{pl} = 4217$ [J/kg K]、$T_{sat} = 100$ [℃]、$Pr = 1.76$、$n = 1$
関連ページ
平板の熱伝達率の計算(強制対流熱伝達)
平板の熱伝達率の計算(自然対流熱伝達)
放射エネルギーの計算(ステファンボルツマンの法則)
円柱の熱伝達率の計算(強制対流熱伝達)
