前回は有限体積法のメッシュについてお話しました。
今回は有限体積の離散化を行って具体的に解くべき方程式を導出してみたいと思います。
目次
コントロールボリュームでの離散化
第2回目で見たように、定常熱伝導方程式を積分形で表すと(4-1)式のようになりました。
$$- \int_{S} (\lambda \nabla T) \cdot d{\bf S} = \int_{V} q dV \tag{4-1}$$
この式をコントロールボリュームについて考えてみましょう。コントロールボリュームはいくつかの面で構成されている微小体積のセルです。
(4-1)式の右辺は体積積分ですが、セル内で発熱量 $q$ は一様であるとすると(※)、
$$\int_{V} q dV = q_c V_c \tag{4-2}$$
となります。$q_c$ はセルの発熱量、$V_c$ はセルの体積です。
一方、(4-1)式の左辺の面積積分は、セルの各面に対して総和をとることと同じなので(※)、
と表せます。添字の $f$ は各面での値を表しています。${\bf S}_f$ は面の面積ベクトルです。面積ベクトルとは、大きさがその面の面積 $S_f$ で方向が面の法線方向であるようなベクトルです。通常はセルに対して外側を向いたベクトルとして定義されます。
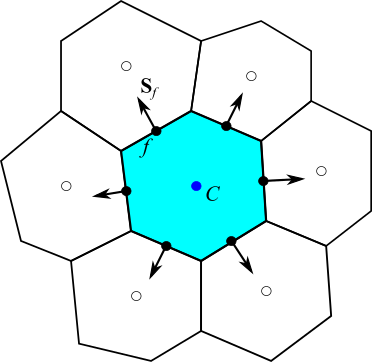
つまり(4-1)式は一つのセルで考えると、次のように表せます。
$$\sum_f (-\lambda \nabla T)_f \cdot {\bf S}_f = q_c V_c \tag{4-4}$$
実はこの式が、定常熱伝導方程式を有限体積法で離散化した最初の基本式となります。
※ 積分の観点で考えると、セルの中心点、面の中心点で値を持っていることに相当します。
メッシュでの離散化
続いて(4-4)式をさらに変形していきましょう。
ここで、具体的なメッシュを考えます。今回は2次元の矩形の問題なので構造格子としましょう。このメッシュは全てのセルが長方形で縦横に規則正しくならんでいるものとします(直交格子といいます)。
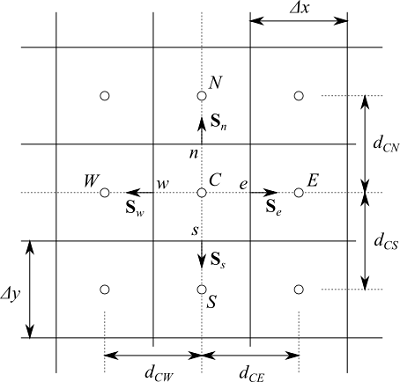
着目するセルを $C$、そのセルを構成している面を $e$、$w$、$n$、$s$ 、各面で隣接するセルを $E$、$W$、$N$、$S$ としましょう(East、West、North、Southの略です)。
セル $C$ に対して(4-4)式を書き下すと、
となります。$e$、$w$、$n$、$s$ の添字は各面での値を表しています。
ここで、面 $e$ について見ていきます。$\nabla T = ( \partial T / \partial x, \partial T / \partial y)$ で、${\bf S}_e = (S_e, 0)$ なので、$x$ 方向の微分だけを用いて、
となります。(4-6)式には温度の $x$ 微分が出てきますが、これは以前出てきた中心差分で表してみましょう。面を挟む2つのセルの値を使って中心差分をとります。
$$\left( \frac{\partial T}{\partial x} \right)_e = \frac{T_E - T_C}{d_{CE}} \tag{4-7}$$
ここで、$d_{CE}$ はセル $C$ の中心とセル $E$ の中心の間の距離です。これを(4-6)式に代入して整理すると次のようになります。
次に、面 $w$ についても同様に、
となります。ここで面積ベクトル $ {\bf S}$ はセルに対して外向きを向いているとして式変形してください。この場合は、$ {\bf S}_w= (-S_w, 0)$ です。
面 $n$、面 $s$ は $y$ 方向を向いた面なので $y$ の微分で表され、同様に整理すると、
となります。
(4-8)式から(4-11)式を(4-5)式に代入して整理すると、次式が得られます。
$$\begin{split} a_E &= -\lambda_e \frac{S_e}{d_{CE}} \\ a_W &= -\lambda_w \frac{S_w}{d_{CW}} \\ a_N &= -\lambda_n \frac{S_n}{d_{CN}} \\ a_S &= -\lambda_s \frac{S_s}{d_{CS}} \\ a_C &= - (a_E + a_W + a_N + a_S) \\ b_C &= q_C V_C \end{split} \tag{4-13}$$
意外とスッキリした式になりました。それにこの式をよく見ると、これまでにやってきた差分法の式とよく似ています。差分法は考えている点と周りの点を用いて離散化しましたが、(4-12)式の形も考えているセル $C$ とその周りのセルの値を用いて表されています。
だとすると、この式がセル数分あるということになるので、差分法のときと同じように連立方程式を解いてやると値が求まりそうです。
実はそのとおりで簡単に言ってしまえば、有限体積法とは(4-12)式のように表される連立方程式を解いて値を求める手法なのです。
形状の値について
ここで、面積や距離、体積など形状の値について抑えておきます。今回の2次元の直交構造格子でセルの幅が $x$ 方向、$y$ 方向でそれぞれ一様であるとします。このセル幅を $\Delta x$、$\Delta y$ とすると、形状の各値は次のようになります。
面積 :
$$\begin{split} S_e = S_w = \Delta y \\ S_n = S_s = \Delta x \end{split} \tag{4-14}$$
距離:
$$\begin{split} d_{CE} = d_{CW} = \Delta x \\ d_{CN} = d_{CS} = \Delta y \end{split} \tag{4-15}$$
体積:
$$V_C = \Delta x \Delta y \tag{4-16}$$
このメッシュ形状であれば、このようにセル幅で形状を簡単に表すことができます。
まとめ
長くなってきたので本日はここまでにします。積分形式の方程式に対して、コントロールボリュームを考え離散化しました。差分法のときと同じような離散化された式を得ることができました。
あとはこの式を解いていくのですが、その前に次回は境界条件の取り扱いについて考えてみたいと思います。
