ベンチュリ管の流量の計算

ベンチュリ管の流量を計算します。管直径と圧力差、流体密度、流量係数を入力してください。流速と流量が計算されます。

計算式

ベンチュリ管（ベンチュリ計）は、ベルヌーイの定理を利用した流量を計測する装置です。

図のように直径が一部で縮小した管を流体が流れる場合、ベルヌーイの定理より収縮部で流速が大きくなり、圧力が低下します。

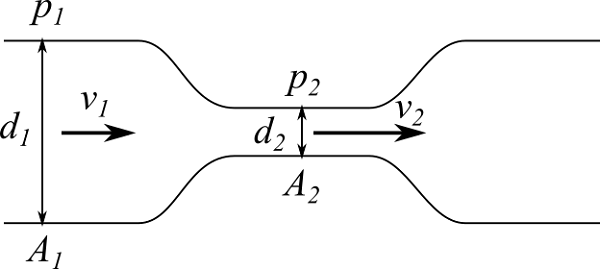
上流側の管直径を$d_1$、流速を$v_1$とし、絞り部の直径を$d_2$、流速を$v_2$とします。この管を水平に置くと、ベルヌーイの定理より、

$$\frac{v_1^2}{2}+\frac{p_1}{\rho} = \frac{v_2^2}{2}+\frac{p_2}{\rho} \tag{1}$$

ここで、$\rho$は流体密度

となります。

この管を流れる流量$Q$は、連続の式（流量保存）より、

$$Q = v_1 A_1 = v_2 A_2 \tag{2}$$

ここで、$A_1=\pi d_1^2/4$、$A_2=\pi d_2^2/4$ は各部の断面積

と書けます。

(1)式と(2)式より、流量$Q$について解くと、

$$Q=A_2 \sqrt{\frac{2 \Delta p}{\rho (1 - (A_2/A_1)^2)}} \tag{3}$$

ここで、$\Delta p = p_1 - p_2$ は圧力差

となります。実際には粘性や壁による摩擦損失があるため、

$$Q=C A_2 \sqrt{\frac{2 \Delta p}{\rho (1 - (A_2/A_1)^2)}} \tag{4}$$

とします。ここで、$C$は流量係数で、0.95～0.99程度の値です[1]。

参考文献[1]　森田泰司. 流体の作用とその応用機械. 東京電機大学出版局, 1970, p. 61-62.