三角形の面積の計算
3次元座標での三角形の面積を計算します。
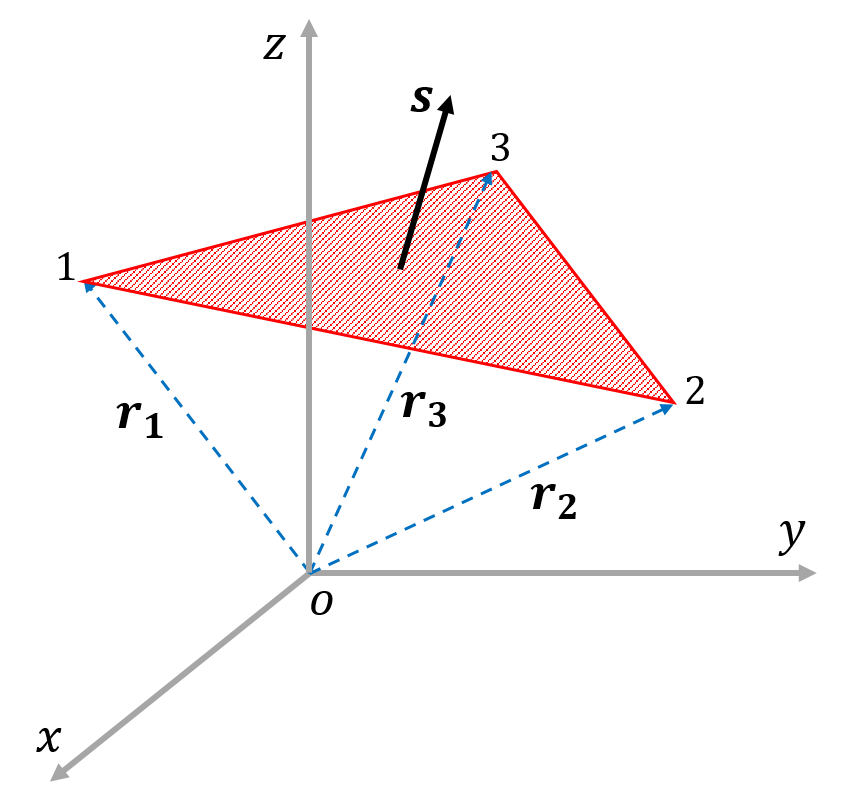
図のような三角形の面積ベクトル $\boldsymbol{s}$（大きさが三角形の面積で、方向が三角形の法線方向となるベクトル）は、以下の式で表されます。
$$ \boldsymbol{s} = \frac{1}{2} \left( \boldsymbol{r_2} - \boldsymbol{r_1} \right ) \times \left( \boldsymbol{r_3} - \boldsymbol{r_1} \right )$$
点1から点2へ向かうベクトル $\boldsymbol{r_2} - \boldsymbol{r_1}$ と点1から点3へ向かうベクトル $\boldsymbol{r_3} - \boldsymbol{r_1}$ のベクトル積が、平行四辺形の面積を表すため、その半分が三角形の面積となります。
点1、2、3の座標を入力してください。面積ベクトルと面積が計算されます。
関連項目
図形の体積・面積を計算できるページです。球、円（円柱、円錐）、四角形（四角柱、四角錐）、三角形（三角柱、三角錐）の各図形の体積や面積を計算します。各図形の形状を入力すると、面積や体積が計算され出力されます。