トリチェリの定理による流出速度と流量の計算

大きなタンクに開いた穴から流出する水の流出速度と流量を、トリチェリの定理により計算します。水深、穴直径、速度係数、収縮係数を入力してください。流出速度と流出流量が計算されます。

計算式

大きなタンクに穴が開いている場合の水の流出速度は、ベルヌーイの定理により求めることができます。

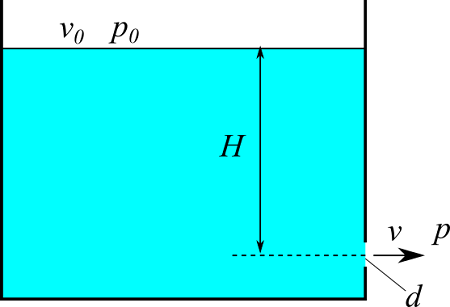
水面の流速を$v_0$、圧力を$p_0$とし、水深$H$の位置に開いた直径$d$の穴から出る水の流速を$v$、圧力を$p$とします。

ベルヌーイの定理を適用すると、

$$\frac{v_0^2}{2}+\frac{p_0}{\rho}+g H = \frac{v^2}{2}+\frac{p}{\rho} \tag{1}$$

となります。いま、穴に対してタンクが十分大きいとすると、$v_0 \simeq 0$と近似でき、$p_0$と$p$は大気圧に等しいので、(1)式は、

$$v = \sqrt{2 g H} \tag{2}$$

となります。これをトリチェリの定理（Torricelli's theorem）といいます。

実際には粘性や壁などの摩擦損失があるため(2)式の速度より低下し、

$$v = C_v \sqrt{2 g H} \tag{3}$$

と書けます。ここで、$C_v$は速度係数で 0.93 ～ 0.98 程度の値です[1]。

また、流量$Q$は、

$$Q=C_c A v = C_v C_c A \sqrt{2 g H} \tag{4}$$

ここで、$A=\pi d^2/4$は穴の面積、$C_c$は収縮係数で0.61～0.66程度の値をとります[1]。収縮係数は穴から噴出する噴流の断面積と穴の面積の比を表します。

参考文献[1]　森田泰司. 流体の作用とその応用機械. 東京電機大学出版局, 1970, p. 63.