前回はSPH法での粒子にかかる力の計算方法について説明しました。
今回はナビエ=ストークス方程式の時間的な解法についてお話します。
Leap-Frog法
これまでの講座で、時間変化を表す微分方程式を解く方法として、オイラー法やルンゲ=クッタ法などをご紹介しました。SPH法のナビエ=ストークス方程式も同じ微分方程式なので、これらの解法を使って解くことはもちろん可能です。
一方で、SPH法ではLeap-Frog法(蛙飛び法)とよばれる手法がよく使われています。
まず、速度を${\bf v}$、位置を${\bf r}$、力を${\bf F}$として、運動方程式
$$\frac{d {\bf v}}{dt} = {\bf F}$$
$$\frac{d {\bf r}}{dt} = {\bf v} \tag{10-1}$$
を考えます。これを、Leap-Frog法では、次のように解きます。
$${\bf v}_{n+1/2} = {\bf v}_{n-1/2} + \Delta t {\bf F}_n $$
$${\bf r}_{n+1} = {\bf r}_n + \Delta t {\bf v}_{n+1/2} \tag{10-2}$$
ここで、$n$は時間ステップ、$\Delta t$は時間刻み幅です。${\bf F}_n$を計算するためには、
$${\bf v}_n = {\bf v}_{n-1/2} + \frac{\Delta t}{2} {\bf F}_{n-1} \tag{10-3}$$
と${\bf r}_n$を使います。
一見、オイラー法に似ていますが、図示すると速度と位置のタイミングが半分ずれて進んでいます。
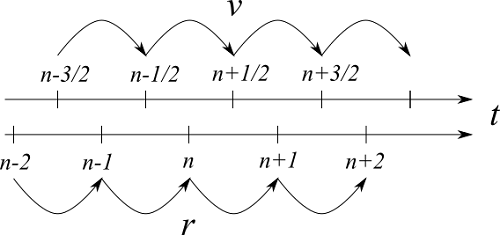
これが「蛙飛び」といわれる所以です。
オイラー法は1次精度でしたが、Leap-Frog法は2次精度です。4次のルンゲ=クッタ法と比べると精度は低いですが、メリットがあります。それはシンプレクティック(symplectic )性と呼ばれるものです。これはいわゆるエネルギー保存性といってよいかと思います。
オイラー法やルンゲ=クッタ法は、時間を進めていくと少なからずエネルギーの誤差が増大します。一方シンプレクティック性を持つLeap-Frog法は誤差の増大が抑えられます。試しに以前計算したばねの運動(講座1-10、講座2-2)で4次のルンゲ=クッタ法とLeap-Frog法でエネルギーの時間推移を比較してみます。減衰のない単振動のばねの運動で、エネルギーの初期からの相対誤差を下図に示します。
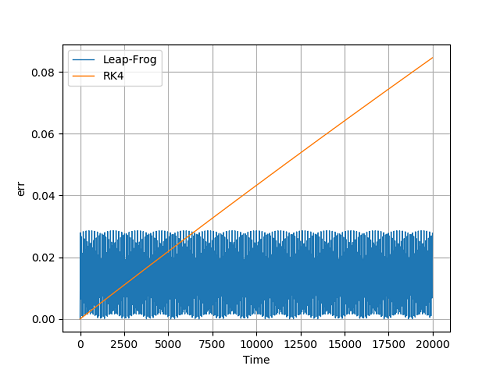
ルンゲ=クッタ法(RK4)は時間とともに誤差が増大しています。一方Leap-Frog法は誤差がある幅に収まっています。このようにLeap-Frog法はエネルギー保存性を持っていることがわかります。ただし、エネルギー保存性があるからといって、必ずしも真の解からの誤差が小さいわけではないので、注意が必要です。4次のルンゲ=クッタ法の方が次数精度が高いので、真値からの誤差は小さいことがあります。
プログラミング
では、今回もJavaScriptでLeap-Frog法のプログラムを作成してみます。
ここでは、関数の名前をmotionUpdateとします。この関数は、一時間ステップの運動を解き、粒子の速度と位置を更新するものです。
function motionUpdate() {
// Leap-Frog
setParticleToCell();
densityPressure();
particleForce();
for (let i = 0, n = p.length; i < n; i++) {
if (!p[i].active) continue;
p[i].velocity2.x += p[i].force.x * timeDelta;
p[i].velocity2.y += p[i].force.y * timeDelta;
p[i].position.x += p[i].velocity2.x * timeDelta;
p[i].position.y += p[i].velocity2.y * timeDelta;
p[i].velocity.x = p[i].velocity2.x + 0.5 * p[i].force.x * timeDelta;
p[i].velocity.y = p[i].velocity2.y + 0.5 * p[i].force.y * timeDelta;
if ((p[i].position.x < regionAll.left)
|| (p[i].position.y < regionAll.bottom)
|| (p[i].position.x > regionAll.right)
|| (p[i].position.y > regionAll.top)) {
p[i].remove();
}
}
}まず最初に、setParticleToCellという関数を呼んでいます。この関数は、空間分割法のバケットに粒子を格納するための関数で、次のように定義されています。
function setParticleToCell() {
cell.clear();
// fluid particle
cell.add(p);
// wall particle
cell.add(pWall);
}cellは、【5-8】章で作成した空間分割法クラスのオブジェクトです。clearメソッドでバケットを空にしたあと、addメソッドで粒子を格納しています。
densityPressure();
particleForce();densityPressureは密度・圧力の計算(【5-7】章)、particleForceは力の計算(【5-9】章)を行います。
for (let i = 0, n = p.length; i < n; i++) {
if (!p[i].active) continue;
p[i].velocity2.x += p[i].force.x * timeDelta;
p[i].velocity2.y += p[i].force.y * timeDelta;
p[i].position.x += p[i].velocity2.x * timeDelta;
p[i].position.y += p[i].velocity2.y * timeDelta;
p[i].velocity.x = p[i].velocity2.x + 0.5 * p[i].force.x * timeDelta;
p[i].velocity.y = p[i].velocity2.y + 0.5 * p[i].force.y * timeDelta;粒子の速度、位置をLeap-Frog法で求める箇所です。すべての流体粒子に対してループして計算します。
velocity2は、$n+1/2$ステップの速度を表すプロパティです。そして、velocityは位置positionと同じ$n+1$ステップでの速度を表しています。このvelocityとpositionを使って次のステップで力が計算されます。
if ((p[i].position.x < regionAll.left)
|| (p[i].position.y < regionAll.bottom)
|| (p[i].position.x > regionAll.right)
|| (p[i].position.y > regionAll.top)) {
p[i].remove();
}ここは、解析領域から外へ出た粒子を除外するための判定です。regionAllは別途定義しますが、矩形の解析領域全体を表すオブジェクトで、left(x座標の最小)、bottom(y座標の最小)、right(x座標の最大)、top(y座標の最大)のプロパティを持っています。p[i].remove()は粒子クラス(class Particle)の中で定義されるメソッドで、次のように定義されます。
remove() {
this.active = false;
}これは【5-7】章で説明したようにactiveプロパティがfalseなら計算対象から除外するためのものです。
Leap-Frog法で運動を解いていくためには、motionUpdate関数を繰り返し実行するだけです。そのために、【5-3】章でお話したp5.jsのdraw関数の中で呼び出せば自動的に繰り返されます。
まとめ
粒子の運動方程式を数値的に解くLeap-Frog法を紹介しました。さて、ここまででSPH法の骨格となる部分は大体できました。
あとは、初期条件や境界条件、粒子の可視化の部分などを作成すれば最初にお見せした計算結果を再現することができます。