今回から「科学技術計算講座」の第2回目のシリーズがスタートです。第1回目では、一分子反応をオイラー法という数値計算法を使いシミュレーションしてみました。計算はPythonで作成したプログラムで行いましたね。
そのときに、オイラー法は計算精度があまりよくないと言いましたが、実際に厳密解から外れて誤差を含んでいることを示しました。そこで、このシリーズではオイラー法よりも精度の高いルンゲ=クッタ法(Runge-Kutta method)という解法を取り上げてみたいと思います。この解法を用いてPythonで、地球の軌道を計算するプログラムを作ってみましょう。どうぞ、お楽しみに。
本日はまず、ルンゲ=クッタ法とはどのようなものかを説明します。
目次
ルンゲ=クッタ法とは
ルンゲ=クッタ法は、1900年頃にドイツの数学者 Carl Runge と Wilhelm Kutta によって考案されました。前回解いたような微分方程式を解くための数値解法として、幅広く使われている方法です。
ルンゲ=クッタ法には多くの派生的な解法がありますが、ここではよく使われている4次のルンゲ=クッタ法(RK4)を扱います。
オイラー法のおさらい
その前に、前回やったオイラー法をおさらいしましょう。次のような微分方程式に対して、
$$\frac{dy}{dt} = f(t, y) \tag{1}$$
オイラー法は次のように表すことができました。
$$y_{n+1} = y_n + \Delta t f(t_n, y_n) \tag{2}$$
$$t_{n+1} = t_n + \Delta t \tag{3}$$
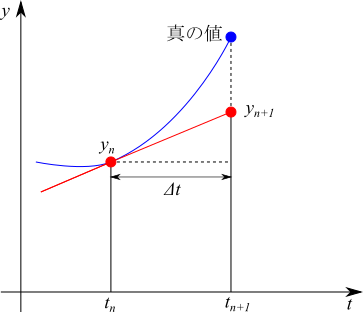
図で表すとこんな感じで、時刻 $t_n$ の傾きを使って、$\Delta t$ 進んだ時刻 $t_{n+1}$ の値 $y_{n+1}$ を求めているんでしたね。この図から明らかなように、$\Delta t$ の間に変化が大きくなるような場合には、誤差が大きくなってしまいます。
では、この図からイメージして、誤差を小さくするにはどうすればよいでしょうか?
そう、傾きをうまく調整すれば真の値に近づきそうです。そうなのです、ルンゲ=クッタ法は傾きを調整して真の値に近づけようというコンセプトになっています。
ルンゲ=クッタ法の手順
早速ですが、ルンゲ=クッタ法の式を見てみます。
いきなり多くの式が出てきてとても難しそうですが、そうでもありません。これをオイラー法と同じように図で表すと次のようになります。
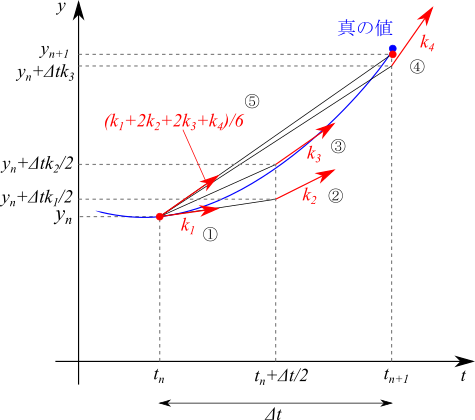
求めたいのは、時刻 $t_{n+1}$ のときの、$y_{n+1}$ の値です。ここで、$k$ というのは傾きを表しています。$y_{n+1}$ を求めるために、いくつかの段階に分けて考えていきます。
① まず、オイラー法と同じように、$t_n$ のときの値 $y_n$ を使って傾き $k_1$ を求めます。
② $k_1$ を使って、$\Delta t / 2$ 進んだ時刻 $t_n+\Delta t / 2$ のときの、値 $y_n + \Delta t k_1 / 2$ を求めます。その値を使って傾き $k_2$ を求めます。
③ $k_2$ を使って、再び $t_n$ から $\Delta t / 2$ 進んだ時刻 $t_n+\Delta t / 2$ のときの、値 $y_n + \Delta t k_2 / 2$ を求めます。その値を使って傾き $k_3$ を求めます。
④ $k_3$ を使って、$t_n$ から $\Delta t$ 進んだ時刻 $t_{n+1}$ のときの、値 $y_n + \Delta t k_3$ を求めます。その値を使って傾き $k_4$ を求めます。
⑤ それぞれの傾きを加重平均した傾き $(k_1 + 2 k_2 + 2 k_3 + k_4) / 6$ を求めます。その傾きを使って、$t_n$ から $\Delta t$ 進んだ時刻 $t_{n+1}$ のときの値を求めます。これが、$y_{n+1}$ になります。
このように、いくつかの傾きから最終的に使う傾きを決めているので、オイラー法のように一つの傾きだけのときよりも、誤差が小さくなりそうだというのがわかると思います。
ルンゲ=クッタ法は傾きの求め方やその数によって、様々な種類が考えられています。ここで説明したのは、4段4次のルンゲ=クッタ法という部類に入ります。ちなみに、オイラー法は1段1次のルンゲ=クッタ法と呼ばれています。なお、これ以降「ルンゲ=クッタ法」というときには、ここで説明した4段4次のルンゲ=クッタ法のことを指します。
プログラムについてはどうでしょうか。(4)~(9)式をプログラミングしていけばよいのです。オイラー法に比べ増えていますが、上から順に計算していくだけなので難しくありません。このように、ルンゲ=クッタ法はプログラミングに向いた方法です。
まとめ
本日はルンゲ=クッタ法について説明しました。一見難しそうですが、図でイメージするとそれほど難しくはありません。プログラミングも簡単そうです。
次回はルンゲ=クッタ法をプログラミングしてみましょう。前シリーズの最後に作ったばねの減衰振動のプログラムをルンゲ=クッタ法にしてみます。そして、オイラー法と比べて精度がどうなっているか確認したいと思います。
