前回は陰解法とそれを解くためのヤコビ法、ガウス=ザイデル法について説明しました。
今回はガウス=ザイデル法を使って完全陰解法をプログラミングします。また時間刻みを大きくとれるか試してみましょう。
目次
熱伝導方程式の完全陰解法形式
前回示したとおり、熱伝導方程式を完全陰解法で書くと次のとおりです。
$$T_i^{n+1} = \frac{1}{1+2c} ( T_i^n + c T_{i+1}^{n+1} + c T_{i-1}^{n+1}) \tag{1}$$
ここで、$c = \alpha \Delta t/ \Delta x^2$。
熱伝導方程式の完全陰解法プログラム
熱伝導方程式を完全陰解法で解くPythonプログラムは次のようになります。以前作ったFTCS法のプログラムを変更していきました。
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
# input parameter
den = 8880.0
cp = 386.0
cond = 398.0
temp_bc = 100.0
temp_init = 0.0
lx = 1.0
nx = 101
tend = 20000.0
dt = 0.1
tout = 100.0
eps = 1.0e-6
itermax = 1000
alpha = cond / (den * cp)
dx = lx / (nx - 1)
nt = int(tend / dt)
nout = int(tout / dt)
ck = alpha * dt / (dx * dx)
#initial condition
temp = np.full(nx, temp_init)
time = 0.0
temp_old = np.zeros(nx)
# Boundary condition
temp[0] = temp_bc # Dirichlet @ x=0
temp[nx-1] = temp[nx-2] # Neumann @ x=Lx
# graph data array
ims = []
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
gx = np.zeros(nx)
for i in range(nx):
gx[i] = i * dx
# time loop
for n in range(1, nt+1):
# full-implicit with Gauss-Seidel
for i in range(nx):
temp_old[i] = temp[i]
for iter in range(itermax):
resd = 0.0
for i in range(1, nx-1):
tp = temp[i]
temp[i] = 1.0 / (1.0 + 2.0 * ck) * (temp_old[i] + ck * temp[i+1] + ck * temp[i-1])
resd += abs(temp[i] - tp)
if resd <= eps:
break
# Boundary condition
temp[0] = temp_bc # Dirichlet @ x=0
temp[nx-1] = temp[nx-2] # Neumann @ x=Lx
time += dt
if n % nout == 0:
print('n: {0:7d}, time: {1:8.1f}, temp: {2:10.6f}, iter: {3:4d}'.format(n, time, temp[nx-1], iter))
im_line = ax.plot(gx, temp, 'b')
im_time = ax.text(0, 110, 'Time = {0:8.1f} [s]'.format(time))
ims.append(im_line + [im_time])
# graph plot
ax.set_xlabel('x [m]')
ax.set_ylabel('Temperature [C]')
ax.grid()
anm = animation.ArtistAnimation(fig, ims, interval=50)
anm.save('animation.gif', writer='pillow')
plt.show()プログラムの説明
変更箇所だけ説明していきます。
eps = 1.0e-6
itermax = 1000eps は収束判定値、itermax はイタレーションの最大回数です。
ck = alpha * dt / (dx * dx)ck は(1)式の $c$ を計算しています。
temp_old = np.zeros(nx)temp_old は(1)式の $T_i^n$ に相当する前の時間ステップの値を格納するための配列です。
# full-implicit with Gauss-Seidel
for i in range(nx):
temp_old[i] = temp[i]
for iter in range(itermax):
resd = 0.0
for i in range(1, nx-1):
tp = temp[i]
temp[i] = 1.0 / (1.0 + 2.0 * ck) * (temp_old[i] + ck * temp[i+1] + ck * temp[i-1])
resd += abs(temp[i] - tp)
if resd <= eps:
break完全陰解法をガウス=ザイデル法で解くメイン部分です。
まず temp_old に前の時間ステップの値を格納します。
次に、forループでガウス=ザイデル法のイタレーションを回します。
その中のforループで空間の各点での(1)式を計算します。resd は前のイタレーションの結果との差の絶対値をとり、全ての点で足し合わせます。resd が eps 以下になればガウス=ザイデル法のforループを抜けます。
print('n: {0:7d}, time: {1:8.1f}, temp: {2:10.6f}, iter: {3:4d}'.format(n, time, temp[nx-1], iter))画面に出力する情報にガウス=ザイデル法のイタレーション回数を加えています。これは出力されたイタレーション回数を見て、最大回数になっていないかチェックするためです。最大回数に達しているようであれば、itermax を大きくします。
計算結果
プログラムをPythonで実行してみてください。計算結果が同じようにアニメーションで出力されたと思います。結果はFTCS法とほぼ同じです。
しかし、計算時間が結構かかりますね。計算結果を見るとガウス=ザイデル法のイタレーションが最大で6回ほどかかっています。陰解法は1回の時間ステップ計算で複数回反復計算をしなければならないため計算量が多くなり、陽解法に比べ時間ステップあたりの計算時間は増えてしまいます。
しかし陰解法にはメリットがあります。陽解法ではCFL条件の厳しい制約があり、時間刻みを大きくとることができませんでした。陰解法ではどうでしょうか。時間刻みを10倍の dt = 1.0 にして計算してみてください。
はい、これも発散せずに計算できましたね。では更に10倍の dt = 10.0 にして計算してみましょう。
なんとこれも計算できました。
このように時間刻みを大きくとっても陰解法は安定に計算できるという特徴があります。前にも言ったように、3次元などで計算点数が多い問題や計算期間の長い問題では、この特徴は大きなメリットです。
陰解法の安定性
陰解法はなぜ、大きな時間刻みでも発散することなく、安定に計算できるのでしょうか。
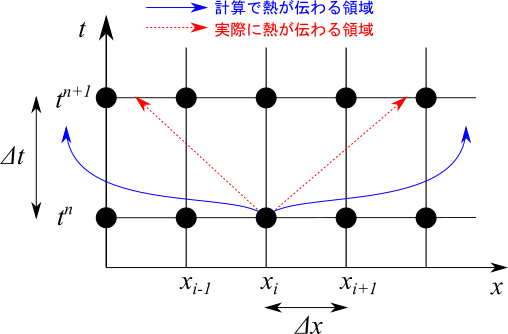
陽解法で安定に解くためには、CFL条件から「計算で情報が伝わる速さ」は「実際に物理量が伝わる速さ」より大きくなっている必要がある、と言いました。
陰解法も同じようにイメージすることができます。陰解法の場合、$T^{n+1}$ を求めるために連立方程式を解く必要があります。その連立方程式には全ての点における $T^n$ の情報が含まれます。逆に言えばある点の $T_i^n$ の情報は、次の時刻 $n+1$ の全ての点に影響を与えることになります。要するに、 陰解法は「計算で情報が伝わる速さ」は「実際に物理量が伝わる速さ」より必ず大きくなり、CFL条件を満たすことになります。
今回解いている(1)式の陰解法も安定性解析を行って数学的に説明できますが、このタイプの陰解法は無条件安定といい理論的にどのような $\Delta t$ に対しても安定であることが証明されています。(ここではやりません。。。)
安定性と精度
陰解法は安定に計算できる解法だということがわかりましたが、最後にひとつ注意しておきます。それは「どんな時間刻みでも計算が発散せず安定に解ける」ということと、「計算精度が高い」ということは全く別の話だということです。例えば、今回時間刻みを変えた結果を並べて見てみましょう。
3600秒後の計算結果を比べてみます。
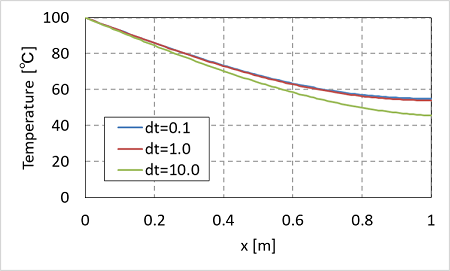
dt = 0.1 と dt = 1.0 の結果はほとんど同じですが、dt = 10.0 の結果は全体的に温度が低くなっています。
陰解法も時間方向に差分をとっている以上、時間刻みが大きいと計算精度が悪くなってしまいます。時間刻みが大きくても安定に計算できるというだけで、精度よく計算できているわけではありません。時間精度をよくしようと思えば、ある程度時間刻みを小さくとる必要があるわけです。
まとめ
熱伝導方程式を完全陰解法で解くプログラムを作成しました。そして大きな時間刻みでも安定に計算できることを確認しました。
次回はもう一つ違う解法をご紹介します。
