平行平板間のクエット流れ・ポアズイユ流れの計算
平行平板間のクエット流れ、ポアズイユ流れの速度分布と流量を計算します。流れタイプと平板間距離、壁面速度、流路長さ、圧力差、粘性係数を入力し[計算実行]ボタンを押してください。最大流速、最大流速位置、流量、速度分布グラフが出力されます。
クエット流れ
層流において、図のように平行平板の上の壁面が速度を持ち圧力勾配が無い場合、クエット流れ(Couette Flow)と呼ばれる流れになります。
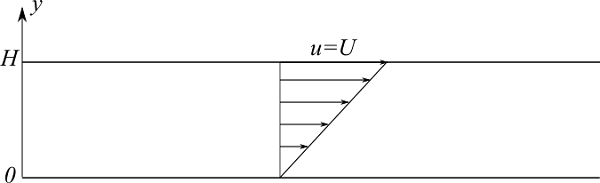
クエット流れの速度分布 $u$ は直線状となり、次式で表されます。
$$ u = U \frac{y}{H} $$
ここで、$U$:壁面速度、$H$:平板間距離。
また流量 $Q$ は、
$$ Q = \frac{UH}{2}$$
となります。
ポアズイユ流れ
層流において壁面が固定された平行平板間を流れる流体は、放物線の速度分布を持ち、ポアズイユ流れ(Poiseuille Flow) と呼ばれます。
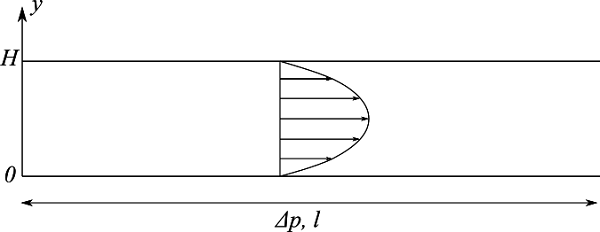
ポアズイユ流れの速度分布 $u$ は以下の式で表されます。
$$ u = -\frac{H^2}{2 \mu} \frac{dp}{dx} \frac{y}{H} (1-\frac{y}{H})$$
ここで、$\mu$:粘性係数、$dp/dx$:圧力勾配。
圧力勾配は、流路長さ $l$、その圧力差 $\Delta p $ を使うと、
$$ - \frac{dp}{dx} = \frac{\Delta p}{l} $$
と書けます。 また、流量 $Q$ は、速度を断面にわたって積分して、
$$Q=-\frac{H^3}{12 \mu} \frac{dp}{dx}$$
となります。
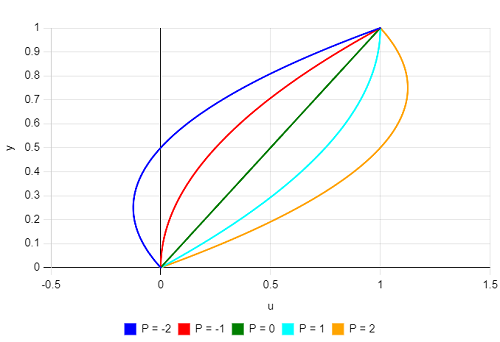
一般に、平板が速度を持ち圧力勾配がある場合は、クエット流れとポアズイユ流れを合成した流れになります。今、
$$P = -\frac{H^2}{2 \mu U} \frac{dp}{dx}$$
とおくと、$P$ により下図のような速度分布となり、$P<-1$で逆流域を持ちます。