ニュートン法による非線形方程式の計算

ニュートン法で非線形方程式の解を求める

ニュートン法（Newton-Raphson Method）で非線形方程式の解を求めます。関数 $f(x)$ と $x$ の範囲を入力し[計算実行]ボタンを押すと、指定した範囲内にある $f(x)=0$ の解を求めることができます。解が複数ある場合は、複数の解が求まります。

使用方法はこちら

関数
範囲	～

結果

軸	最小	最大	刻み	対数
x
y

使い方

１．関数欄に、x を変数とした関数 $f(x)$ を入力します。

２．範囲欄で、求めたい解 x の範囲を指定します。

３．[計算実行]を押すと計算が実行され、結果欄に結果データとグラフが表示されます。

求まる解は、$f(x) = 0$ の方程式の解です。ここでは指定した範囲内にある複数の解を求めることができます。

関数の入力

関数は、xを変数として入力します。使用できる演算子、数学関数は以下のとおりです。入力は半角で行ってください。

数式	名称	入力形式
$+$	加算	+
$-$	減算	-
$\times$	乗算	*
$\div$	除算	/
$( )$	括弧	( )
$x^a$	べき乗	x^a
$\sin x$	正弦	sin(x)
$\cos x$	余弦	cos(x)
$\tan x$	正接	tan(x)
$\sin^{-1} x$	逆正弦	asin(x)
$\cos^{-1} x$	逆余弦	acos(x)
$\tan^{-1} x$	逆正接	atan(x)

数式	名称	入力形式
$\sinh x$	双曲正弦	sinh(x)
$\cosh x$	双曲余弦	cosh(x)
$\tanh x$	双曲正接	tanh(x)
$\sinh^{-1} x$	逆双曲正弦	asinh(x)
$\cosh^{-1} x$	逆双曲余弦	acosh(x)
$\tanh^{-1} x$	逆双曲正接	atanh(x)
$e^x$	指数関数	exp(x)
$\ln{x}$	自然対数	log(x)
$\log_{10} x$	常用対数	log10(x)
$\sqrt{x}$	平方根	sqrt(x)
$\|x\|$	絶対値	abs(x)
$\pi$	円周率	pi

関数入力の例

関数式	入力形式
$x^2+3x-5$	x^2+3*x-5
$\sin x + e^{-x/10}$	sin(x)+exp(-x/10)
$x+\sqrt{x}-2 \pi$	x+sqrt(x)-2*pi

結果

結果データ

結果欄に結果データが出力されます。関数、xの範囲、解の数、解xの各データが表示されます。

結果データ保存：　表示されている結果データが、solution.txt というファイル名で保存されます。

グラフ

グラフは、関数データが青線、解が赤ポイントで表示されます。

軸ｘ, y：　軸の「最小」「最大」「刻み」を指定できます。指定しない場合は自動で表示されます。「対数」にチェックを入れると対数表示されます。

グラフ表示：　軸設定などを変更した場合は、[グラフ表示]ボタンを押すとグラフが再描画されます。

画像保存：　表示されているグラフが graph.png というファイル名でPNG形式で保存されます。

ニュートン法

非線形方程式の解法はニュートン法（Newton-Raphson Method）を使用しています。ニュートン法は方程式

$$f(x) = 0$$

の解を求めるための数値解法です。$f(x)$のゼロ点が求まります。ニュートン法では、次の式を反復的に解いて解を求めます。

$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$$

$f'(x)$は、関数 $f(x)$ の導関数。

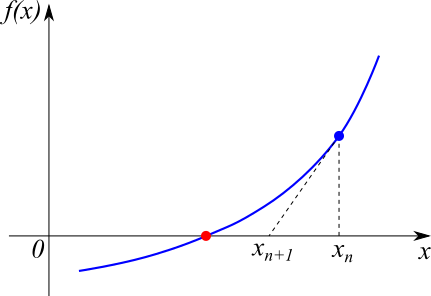
通常、ニュートン法は与えた初期値に対して一つの解が求まりますが、ここでは指定した範囲内にある複数の解を探索して求めています。

※ニュートン法は反復計算による近似解を求めるため、解は微小な誤差を含んでいる場合があります。
※関数の形（範囲内に解が多すぎる、解が接近しすぎているなど）によって解が求まらない場合があります。その場合はグラフを見ながら範囲を調整してみてください。
※このプログラムは虚数解には対応していません。実数解を持たない場合は、解を求めることはできません。