今回は行列のLU分解について解説します。
正方行列${\bf A}$が与えられたとき、この行列を下三角行列${\bf L}$と上三角行列${\bf U}$の積に分解することをLU分解といいます。
$${\bf A}={\bf L}{\bf U} \tag{1}$$
下三角行列とは行列の下半分の三角部分にのみ非ゼロの要素があり、上半分の三角部分は全てゼロである行列です。
$${\bf L}=\left(\begin{array}{ccccc} 1 & 0 & 0 & \cdots & 0 \\ l_{21} & 1 &0 &\cdots & 0 \\ l_{31} & l_{32} &1 &\cdots & 0 \\ \vdots & \vdots & \vdots &\ddots &0 \\ l_{N1}& l_{N2} & l_{N3} &\cdots & 1 \end{array}\right) \tag{2}$$
上三角行列は逆に、上半分の三角部分のみ非ゼロで、下半分はゼロである行列です。
$${\bf U}=\left(\begin{array}{ccccc} u_{11} & u_{12} & u_{13} & \cdots & u_{1N} \\ 0 & u_{22} &u_{23} &\cdots & u_{2N} \\ 0 &0 &u_{33} &\cdots & u_{3N} \\ \vdots & \vdots & \vdots &\ddots & \vdots \\ 0&0 & 0 &0& u_{NN} \end{array}\right) \tag{3}$$
ここで各行列を一意的に決めるために、行列${\bf L}$の対角成分は全て1とします。${\bf U}$の対角成分を1としてもよいですが、ここでは${\bf L}$の方を1とします。
LU分解は線形方程式を解くためによく使われます。
次の線形方程式系
$${\bf A}{\bf x} = {\bf y} \tag{4}$$
があるとします。${\bf A}={\bf L}{\bf U}$でLU分解できたとすると、(4)式は
$${\bf L}{\bf U}{\bf x}={\bf y} \tag{5}$$
となります。さらに(5)式は
$${\bf L}{\bf z}={\bf y} \tag{6}$$
$${\bf U}{\bf x}={\bf z} \tag{7}$$
の2式に分けることができます。(6)、(7)式は後で詳細に述べますが簡単に解くことができます。
実際の問題では行列${\bf A}$に対して異なる${\bf y}$で何度も(4)式を解かなければならないことがあります。その場合、一度LU分解しておけば(6)、(7)式より素早く解を求めることができます。
また${\bf A}$の逆行列や行列式を求めるときにも、LU分解されていると便利です。
逆行列は、
$${\bf A}^{-1}={\bf U}^{-1}{\bf L}^{-1} \tag{8}$$
行列式は、
$$|{\bf A}|=|{\bf L}||{\bf U}|\tag{9}$$
で計算できます。
三角行列の逆行列や行列式は簡単に求めることができるので、これをもとに${\bf A}$の逆行列や行列式を計算することができます。
具体的にLU分解の過程を見ていきましょう。LU分解にはいろいろな方法がありますが、ここでは二つ紹介します。
簡単のために3×3の行列を考えます。${\bf A}={\bf L}{\bf U}$は各成分で書き下すと次のように書けます。
$$\begin{split} \left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33} \end{array}\right) &= \left(\begin{array}{ccc} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\l_{31} & l_{32} &1 \end{array}\right) \left(\begin{array}{ccc} u_{11} & u_{12} & u_{13} \\ 0& u_{22} & u_{23} \\0 & 0 & u_{33} \end{array}\right) \\ &=\left(\begin{array}{ccc} u_{11} & u_{12} & u_{13} \\ l_{21} u_{11} & l_{21} u_{12} + u_{22} & l_{21} u_{13} + u_{23} \\l_{31} u_{11} & l_{31} u_{12} + l_{32} u_{22} & l_{31} u_{13} + l_{32} u_{23} + u_{33} \end{array}\right) \end{split} \tag{10}$$
この式から、$l$、$u$について解くと、第1行目より、
$$\begin{split} u_{11} &= a_{11} \\ u_{12} &= a_{12} \\ u_{13} &= a_{13} \end{split} \tag{11}$$
第2行目より、
$$\begin{split} l_{21} &= \frac{a_{21}}{u_{11}} \\ u_{22} &= a_{22} -l_{21} u_{12}\\ u_{23} &= a_{23} -l_{21} u_{13} \end{split} \tag{12}$$
第3行目より、
$$\begin{split} l_{31} &= \frac{a_{31}}{u_{11}} \\l_{32} &= \frac{a_{32}-l_{31} u_{12}}{u_{22}}\\ u_{33} &= a_{33} -l_{31} u_{13} -l_{32} u_{23}\end{split} \tag{13}$$
となります。上から順に求めていくと、全ての$l$、$u$が求まります。
これを一般的に書くと次のようになります。
$$\begin{split} l_{ij} &= \frac{a_{ij}-\sum_{k=1}^{j-1} l_{ik} u_{kj}}{u_{jj}} \qquad & (j = 1 \sim i-1) \\ u_{ij} &= a_{ij} - \sum_{k=1}^{i-1} l_{ik} u_{kj} & (j = i \sim N) \end{split} \tag{14}$$
これはDoolittleのアルゴリズム と呼ばれています(なお、上三角行列${\bf U}$の対角成分を1にする方法はCroutのアルゴリズム といいます)。
では、Python でDoolittleのLU分解をプログラミングしてみましょう。
#LU decomposition - Doolittle algorithm
for i in range(1, n):
# L
for j in range(i):
for k in range(j):
a[i][j] -= a[i][k] * a[k][j]
a[i][j] /= a[j][j]
#U
for j in range(i, n):
for k in range(i):
a[i][j] -= a[i][k] * a[k][j] 行列${\bf A}$を2次元配列a としています。ここではメモリ節約のために行列${\bf L}$と${\bf U}$を別の配列として定義せず、もとの配列a を更新して書き換えることで計算結果を格納しています。結果としてa は次のような${\bf L}$と${\bf U}$を合わせた行列になっています。
$$\left(\begin{array}{ccccc} u_{11} & u_{12} & u_{13} & \cdots & u_{1N} \\ l_{21} & u_{22} &u_{23} &\cdots & u_{2N} \\ l_{31} &l_{32} &u_{33} &\cdots & u_{3N} \\ \vdots & \vdots & \vdots &\ddots & \vdots \\ l_{N1}&l_{N2} & l_{N3} & \cdots & u_{NN} \end{array}\right) \tag{15}$$
※式で書くと行列の添字は1から始まっていますが、Pythonのプログラムでは配列の添字は0から始まっていることに注意してください。
※LU分解の過程で行列の対角成分で割る操作がでてきます。もし対角成分がゼロだとゼロ割りが起こり計算できなくなります。これに対する処理は以下の記事で説明しています。
部分ピボット選択付きLU分解LU分解について解説します。部分ピボット選択付きのLU分解をPythonプログラムを交えて説明します。また、この行列を用いた線形方程式の解き方も説明しています。
次にガウスの消去法 を用いて、もとの行列を変形していく方法を紹介します。
(10)式において、第2行目を第1行の値を用いて消去していくと、
$$\begin{split} l_{21} &= \frac{a_{21}}{u_{11}} \\ u_{22} &= a_{22} -l_{21} u_{12}\\ u_{23} &= a_{23} -l_{21} u_{13} \end{split} \tag{16}$$
となります。同様に、第3行目を第1行の値を用いて消去していくと、
$$\begin{split} &l_{31} = \frac{a_{31}}{u_{11}} \\&l_{32} u_{22}=a_{32}-l_{31} u_{12} = a'_{32} \\ &l_{32} u_{23} + u_{33} = a_{33} -l_{31} u_{13}= a'_{33}\end{split} \tag{17}$$
となります。次に、第3行目((17)式)の2式目以降を第2行目((16)式)を用いて消去します。
$$\begin{split} l_{32} &= \frac{a'_{32}}{u_{22}} \\u_{33}&=a'_{33}-l_{32} u_{23} \end{split} \tag{18}$$
これをPythonでプログラムすると
#LU decomposition - right-looking algorithm
for k in range(n-1):
for i in range(k+1, n):
a[i][k] = a[i][k] / a[k][k]
for j in range(k+1, n):
a[i][j] -= a[i][k] * a[k][j] と書けます。Doolittleの方法よりプログラム上はずいぶんシンプルです。
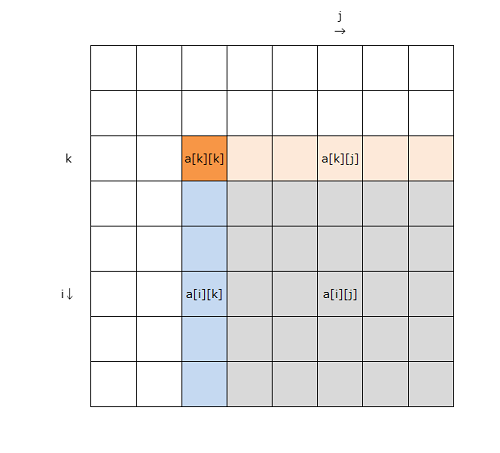
この操作を図示してみます。
k 行目のa[k][k] でa[i][k] を割って青色部分を求めます。これと既知のa[k][j] (ピンク色の部分)を用いて、a[i][j] (灰色部分)を求めていきます。このように右側の部分が更新されていくので、right-lookingアルゴリズム と呼ばれています。
最後に、LU分解を用いて線形方程式(連立一次方程式)を解く方法について説明します。
前述のとおり、(6)(7)式を用いると解を求めることができます。まず(6)式を成分で書き下すと、
$$\begin{split} &z_1 = y_1 \\&l_{21}z_1+z_2 = y_2 \\ &l_{31}z_1+l_{32}z_2 +z_3= y_3\\& \cdots \\& l_{N1}z_1+l_{N2}z_2 +l_{N3}z_3+\cdots + z_N= y_N \end{split} \tag{19}$$
となります。これは一番上から$z$の値を求めて順次代入していけば次のように簡単に全ての$z$を求めることができます。
$$\begin{split} &z_1 = y_1 \\&z_2 = y_2-l_{21}z_1 \\ &z_3= y_3-l_{31}z_1-l_{32}z_2 \\& \cdots \\& z_N= y_N -l_{N1}z_1-l_{N2}z_2 -\cdots-l_{NN-1}z_{N-1}\end{split} \tag{20}$$
これを前進代入 といいます。
同様に(7)式を書き下すと、
$$\begin{split} &u_{11}x_1+u_{12}x_2 +\cdots + u_{1N}x_N= z_1\\&u_{22}x_2 +u_{23}x_3+\cdots + u_{2N}x_N= z_2 \\&u_{33}x_3+u_{34}x_4+\cdots + u_{3N}x_N= z_3 \\ & \cdots \\& u_{NN}x_N= z_N \end{split} \tag{21}$$
となり、今度は一番下から逆向きに$x$の値を求めて代入していけば、
$$\begin{split} &x_1= \frac{z_1 -(u_{12}x_2 +\cdots + u_{1N}x_N)}{u_{11}}\\&x_2 =\frac{ z_2 - ( u_{23}x_3+\cdots + u_{2N}x_N)}{u_{22}}\\& x_3= \frac{z_3 - (u_{34}x_4+\cdots + u_{3N}x_N)}{ u_{33}} \\ & \cdots \\& x_N= \frac{z_N}{u_{NN}}\end{split} \tag{22}$$
同じく全ての$x$を求めることができます。これを後退代入 といいます。
これもPythonプログラムの例を載せておきます。
#LUx=y -> x
#Lz=y
for i in range(1, n):
for j in range(i):
x[i] -= a[i][j] * x[j]
#Ux=z
for i in range(n-1, -1, -1):
for j in range(i+1, n):
x[i] -= a[i][j] * x[j]
x[i] /= a[i][i] ここでは前述のように${\bf L}$と${\bf U}$行列が合わさった行列a に対して計算を行います。x 配列は最初に${\bf y}$の値が格納されており、最終的に求める解${\bf x}$に更新されます。
このようにLU分解が出来ていると前進代入、後退代入の操作で簡単に線形方程式の解を求めることができます。
今回は行列のLU分解についてお話しました。当サイトの以下のページでは与えた行列のLU分解ができますので試してみてください。
行列計算のオンラインツールです。行列の行列式、逆行列、ランク、LU分解、部分ピボット選択LU分解、QR分解の計算ができます。行列を入力して計算項目を選択し、[計算実行]ボタンを押すと計算結果が表示されます。実数、複素数どちらにも対応しています。
また共役勾配法の前処理行列を求める際などでもLU分解は使われます。
前処理行列の求め方について解説します。対角スケーリング、不完全コレスキー分解、不完全LU分解についてPythonプログラムを交えながら説明しています。
実用的な数値計算分野でもよく使われるので、理解しておくとよいかもしれません。
全体の目次