以前、行列のLU分解について解説しました。
今回は部分ピボット選択付きLU分解について説明します。
目次
ピボット選択付きLU分解
次のような行列のLU分解を考えます。
$${\bf A}=\left(\begin{array}{ccc} 0 & 3 & 1 \\ 1 & -2 &3 \\-2 & 1 & 4 \end{array}\right) \tag{1}$$
以前示したLU分解の方法は行列の対角成分で割るという操作が入るため、この行列の$a_{11}$成分で割ろうとするとゼロ割となって計算できなくなってしまいます。
そこで、1行目を他の行と交換した行列を考えLU分解を進めます。このとき、0である対角成分より下にある同じ列の中から絶対値が一番大きな要素の行と交換します。
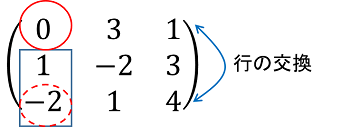
今の場合は、-2である$a_{31}$要素が絶対値が一番大きいので、3行目と1行目を交換します。
$$\left(\begin{array}{ccc} -2 & 1 & 4\\ 1 & -2 &3 \\0 & 3 & 1 \end{array}\right) \tag{2}$$
このような交換操作をピボット選択(pivoting)といいます。今回のように行列の行だけを入れ替えるのを部分ピボット選択(partial pivoting)、行も列も入れ替える操作を完全ピボット選択(full pivoting)といいます。ここではよく使われる部分ピボット選択について詳しく見ていきます。
なお、対象となる対角要素がゼロでなくても、他の要素に比べ非常に小さい場合は、割り算により係数が大きくなってしまい桁落ちなどの数値誤差が生じやすくなります。そのような誤差を防ぐためにもピボット選択は有効です。
LU分解は最終的には行を交換した行列に対して行われます。この行列の行を交換するための変換行列を${\bf P}$とすると、
$${\bf P}{\bf A} = {\bf L} {\bf U} \tag{3}$$
が成り立ちます。ここで${\bf P}$は置換行列(permutation matrix)と呼ばれ次のような単位行列に似た形をしています。
$${\bf P}=\left(\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 &0\\0 & 1 & 0 \end{array}\right) \tag{4}$$
この行列を見ると単位行列の3行目が1行目に、1行目が2行目に、2行目が3行目に入れ替わっています。実際に(1)式の行列${\bf A}$に左から(4)式の${\bf P}$を掛けると同じように行が入れ替わることがわかります。
$${\bf P}{\bf A}=\left(\begin{array}{ccc} -2 & 1 & 4 \\0 & 3 & 1 \\1 & -2 &3 \end{array}\right) \tag{5}$$
このように置換行列は行の入れ替えの操作を行うための行列です。
※もちろん${\bf P}$は(4)式の行列以外にもいくつかパターンがあります。例えば1行目を2行目と入れ替える場合など。
部分ピボット選択付きLU分解のプログラム
では、Pythonで部分ピボット選択付きLU分解のプログラムを作りましょう。ここでは以前紹介したright-lookingアルゴリズムによるLU分解に対して、部分ピボット選択を付け加えます。
#LU decomposition with partial pivoting- right-looking algorithm
for i in range(n):
p[i] = i
for k in range(n-1):
pivot = k
amax = abs(a[pivot][k])
for i in range(k+1, n):
if abs(a[i][k]) > amax:
pivot = i
amax = abs(a[pivot][k])
if pivot != k:
for i in range(n):
tmp = a[k][i]
a[k][i] = a[pivot][i]
a[pivot][i] = tmp
tmp = p[k]
p[k] = p[pivot]
p[pivot] = tmp
for i in range(k+1, n):
a[i][k] /= a[k][k]
for j in range(k+1, n):
a[i][j] -= a[i][k] * a[k][j]まず最初のforループで配列pにそのインデックスを代入しています。
for i in range(n):
p[i] = i配列pはベクトルの形にしていますが、置換行列${\bf P}$を表しています。行列の形にしてもよいですが、今回はどの行がどの行に交換されたかが分かりさえすればよいので、ベクトルの形で定義します。最初は置換されていないので、インデックスをそのまま代入しています。これで行番号が順に入力されたことになります。
次はLU分解の実行部分に入ります。
pivot = k
amax = abs(a[pivot][k])
for i in range(k+1, n):
if abs(a[i][k]) > amax:
pivot = i
amax = abs(a[pivot][k])最初の箇所は、対象とする行kより下の行iにおける列kの中から絶対値が最大である要素を見つけています。pivot変数にはその行番号が入力されます。
次に、見つかったpivot行とk行を入れ替える操作を行います。
if pivot != k:
for i in range(n):
tmp = a[k][i]
a[k][i] = a[pivot][i]
a[pivot][i] = tmp
tmp = p[k]
p[k] = p[pivot]
p[pivot] = tmpif文はpivotとkが同じ場合は入れ替えを行わなくてよいので、そのための判定です。交換は行列要素aと置換ベクトルpに対して行います。
交換が済んだら、あとは通常のLU分解を行います。これで(3)式のLU分解ができたことになります。
線形方程式の解法
部分ピボット選択を行ったLU行列を用いて線形方程式を解いてみましょう。線形方程式
$${\bf A}{\bf x}={\bf y} \tag{6}$$
に対して、置換行列${\bf P}$を左から掛けます。
$${\bf P}{\bf A}{\bf x}={\bf P}{\bf y} \tag{7}$$
この式に(3)式を代入すると、
$${\bf L}{\bf U}{\bf x}={\bf P}{\bf y} \tag{8}$$
となります。これで以前行ったように、前進代入と後退代入を使って解くことができます。
Pythonのプログラムをあげておきます。
#LUx=Py -> x
#Py
for i in range(n):
x[i] = y[p[i]]
#Lz=Py
for i in range(1, n):
for j in range(i):
x[i] -= a[i][j] * x[j]
#Ux=z
for i in range(n-1, -1, -1):
for j in range(i+1, n):
x[i] -= a[i][j] * x[j]
x[i] /= a[i][i] 最初のfor文で${\bf P}{\bf y}$を求めるため、置換ベクトルpを用いてyベクトルの要素の交換を行っています。
あとは通常の前進代入と後退代入と同じです。
まとめ
今回は部分ピボット選択付きのLU分解についてお話しました。当サイトの以下のページでは、このLU分解を行うことができるのでぜひ試してみてください。

