今回は有限体積法で勾配を計算する方法の中で、最小二乗法を使って計算する方法について説明します。
Green-Gaussの定理による勾配計算法は以下の記事を参照ください。
有限体積法で勾配を計算する方法について解説します。ここでは、Green-Gaussの定理にもとづく勾配の計算方法について説明しています。面の値の計算方法もセルと節点にもとづく方法を紹介します。
最小二乗法
最小二乗法(Least Squares Method)とは、あるデータの組$(x_i, y_i)$に対して、モデル関数$y=f(x)$を仮定したとき、
$$J=\sum_i (y_i - f(x_i))^2 \tag{1}$$
が最小となるような$f(x)$を求める方法です。
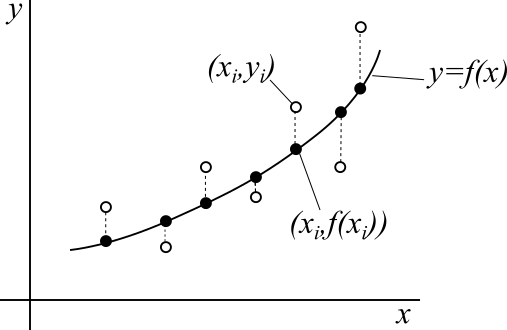
これは、$y_i$とモデル関数で想定される値$f(x_i)$の誤差の二乗和が最小になることを意味します。
ここで、$f(x)$が、
$$f(x)=\sum_k a_k g_k(x) \tag{2}$$
のように、未知の係数$a_k$と既知の関数$g_k(x)$の線形結合によって与えられるとします。$g_k(x)$は既知なので、最小二乗法は未知の$a_k$を求めることに帰着します。
(1)式を最小にするには、$J$を$a_k$で偏微分したものが0(極値となる)という条件、
$$ \frac{\partial J}{\partial a_0} = \frac{\partial J}{\partial a_1} = \cdots = \frac{\partial J}{\partial a_k} = 0 \tag{3}$$
を課してやります。
(3)式は、$a_k$に対する連立方程式となるため、これを解くと$a_k$が求まります。
最小二乗法による勾配計算
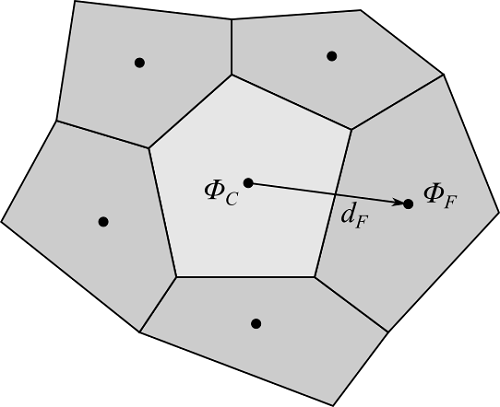
最小二乗法をセルの勾配計算に適用するには、まずセル$C$に隣接するセル$F$の値$\phi_F$を、セル$C$の勾配$\nabla \phi_C$を用いて次のように仮定します。
$$\phi_F = \phi_C + \nabla \phi_C \cdot {\bf d}_F \tag{4}$$
ここで、${\bf d}_F = {\bf x}_F - {\bf x}_C$、${\bf x}$は位置ベクトル
これは、$F$の値が勾配$\nabla \phi_C$により線形に表せるとしたものです。
ここで、(4)式を(1)式の$f(x_i)$として最小二乗法を適用します。
$$J=\sum_F \{w_F (\phi_F - (\phi_C + \nabla \phi_C \cdot {\bf d}_F))\}^2 \tag{5}$$
(5)式はセル$C$に隣接する全てのセル$F$に対して和をとっています。$w_F$は、重み係数でセル$F$の寄与に重みをつけるために導入します。
(5)式を3次元成分で書き下します。
$$J=\sum_F w_F^2 \left(\phi_F - \phi_C - \left(\left. \frac{\partial \phi}{\partial x} \right|_C d_x + \left. \frac{\partial \phi}{\partial y} \right|_C d_y + \left. \frac{\partial \phi}{\partial z} \right|_C d_z \right) \right)^2 \tag{6}$$
ここで、${\bf d}_F = (d_x, d_y, d_z)$。
(6)式において、未知数は$\partial \phi / \partial x |_C$、$\partial \phi / \partial y |_C$、$\partial \phi / \partial z |_C$の勾配部分です。
最小二乗法を適用するために、次のように(3)式の条件を課します。
$$ \frac{\partial J}{\partial (\frac{\partial \phi}{\partial x}|_C)} = \frac{\partial J}{\partial (\frac{\partial \phi}{\partial y}|_C)} = \frac{\partial J}{\partial (\frac{\partial \phi}{\partial z}|_C)} = 0 \tag{7}$$
(7)式に(6)式を代入し整理すると、次の3式となります。
$$\sum_F w_F^2 d_x \left(\left. \frac{\partial \phi}{\partial x} \right|_C d_x + \left. \frac{\partial \phi}{\partial y} \right|_C d_y + \left. \frac{\partial \phi}{\partial z} \right|_C d_z \right) = \sum_F w_F^2 d_x (\phi_F - \phi_C) \tag{8}$$
$$\sum_F w_F^2 d_y \left(\left. \frac{\partial \phi}{\partial x} \right|_C d_x + \left. \frac{\partial \phi}{\partial y} \right|_C d_y + \left. \frac{\partial \phi}{\partial z} \right|_C d_z \right) = \sum_F w_F^2 d_y (\phi_F - \phi_C) \tag{9}$$
$$\sum_F w_F^2 d_z \left(\left. \frac{\partial \phi}{\partial x} \right|_C d_x + \left. \frac{\partial \phi}{\partial y} \right|_C d_y + \left. \frac{\partial \phi}{\partial z} \right|_C d_z \right) = \sum_F w_F^2 d_z (\phi_F - \phi_C) \tag{10}$$
(8)~(10)式を行列の形で書くと、
$$\left(\begin{array}{ccc} \sum w_F^2 d_x d_x & \sum w_F^2 d_x d_y & \sum w_F^2 d_x d_z \\ \sum w_F^2d_y d_x & \sum w_F^2 d_y d_y & \sum w_F^2 d_y d_z \\ \sum w_F^2 d_z d_x & \sum w_F^2 d_z d_y & \sum w_F^2 d_z d_z \end{array}\right) \left(\begin{array}{c} \partial \phi / \partial x |_C \\ \partial \phi / \partial y |_C \\ \partial \phi / \partial z |_C \end{array}\right) = \left(\begin{array}{c} \sum w_F^2 d_x (\phi_F - \phi_C) \\ \sum w_F^2 d_y (\phi_F - \phi_C) \\ \sum w_F^2 d_z (\phi_F - \phi_C) \end{array}\right) \tag{11}$$
となります。(11)式は3×3行列の線形方程式で、容易に解くことができ、これにより勾配が求まります。
ここで重み係数$w_F$について考えます。
もし、$w_F=1$であれば隣接セルごとの寄与が一律になります。中心位置までの距離が同じセル同士が隣接している場合は、これで問題ありません。しかし、大きさの違うセルが隣接している場合、近くに中心が位置するセルも、遠くに中心が位置するセルも同じ寄与度を持つことになります。
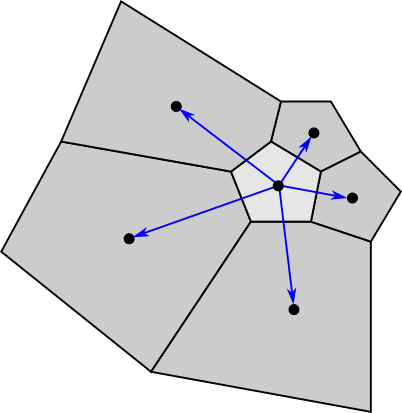
これはつまり、遠くに中心が位置するセルからの影響が過大になることを意味します。誤差関数$J$を考えるうえでは、近くに中心があるセルからの影響を強く受けた方がより精度がよくなると考えられます。そのため、
$$w_F = \frac{1}{|{\bf d}_F|} \tag{12}$$
のように距離で重み付けする係数を考えます。こうすると、遠くに中心があるセルからの寄与が小さく、近くに中心があるセルからの寄与が大きくなります。
まとめ
今回は、最小二乗法によるセル勾配の計算方法について解説しました。多くの汎用流体解析ソフトでは、最小二乗法による勾配計算も選択することができます。普段、ソフトを使用する上で、勾配計算の設定まで意識することはないかもしれませんが、計算方法を知った上で手法の違いで結果がどの程度変わるか確かめておくとよいかも知れません。
全体の目次




