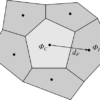
今回は有限体積法で勾配を計算する方法について説明します。
目次
勾配
有限体積法の流体解析などでは、物理量の勾配が必要になることがよくあります。圧力勾配や速度勾配、温度勾配など基礎式の中にも頻繁に出てきます。
物理量$\phi$がセル中心で定義されている場合、そのセルでの$\phi$の勾配を考えてみます。まず簡単のために1次元としましょう。
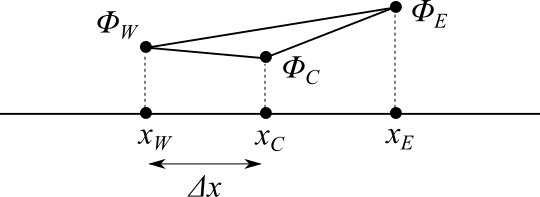
勾配は傾きなので、隣のセルの値とセル幅を使って次のように書くことができます。
構造格子であれば3次元でも同様に表すことができます。しかし、非構造格子など任意のセルの場合はどのように勾配を求めればよいでしょうか。
Green-Gaussの勾配
任意形状のセルの勾配を計算するには、Green-Gauss(グリーン=ガウス)の定理を使います。これはガウスの発散定理から導けますが、勾配に関して体積積分と面積積分を関係付けるものです。
$$\int_{V} \nabla \phi dV = \int_{S} \phi d {\bf S} \tag{2}$$
ガウスの発散定理はこちらも参照ください。
(2)式を実際のセルに適用すると、左辺はセル中心の勾配$\nabla \phi_C$で体積積分して、
$$\int_{V} \nabla \phi dV =\nabla \phi_C V_C \tag{3}$$
ここで、$V_C$:セルの体積
右辺の面積積分は、面の値$\phi_f$としてセルを構成する面で和をとると、
$$\int_{S} \phi d {\bf S} = \sum_f \phi_f {\bf S}_f \tag{4}$$
ここで、${\bf S}_f $:面の面積ベクトル
となります。よって、(2)式からセルの勾配は、
$$\nabla \phi_C = \frac{1}{V_C} \sum_f \phi_f {\bf S}_f \tag{5}$$
で求めることができます。
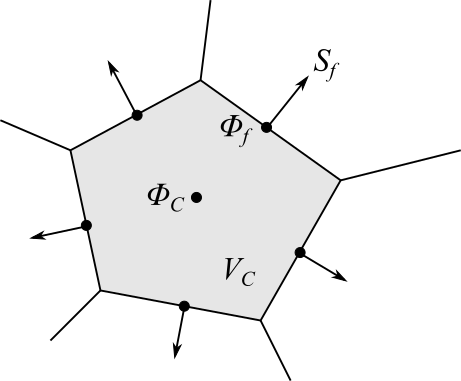
要するに、面の値が分かればセルの勾配を計算することができるというわけです。
面の値の計算
次に面の値をどのように計算するかが問題となります。
セルの値から求める
これはいくつか方法がありますが、ひとつは面を挟むセルの値から線形補間で求める方法です。
$$\phi_e = g \phi_C + (1 - g) \phi_E \tag{6}$$
ここで、$g = |x_e - x_E| / |x_C- x_E|$
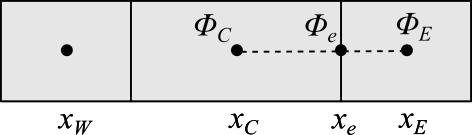
セル幅が一定の構造格子であれば、$g=1/2$となるので、面を挟むセルの値の平均値が面の値となります。
非構造格子の場合は、セルの歪みにより、面を挟むセル中心をむすんだ線上に、面中心がこない場合があります。
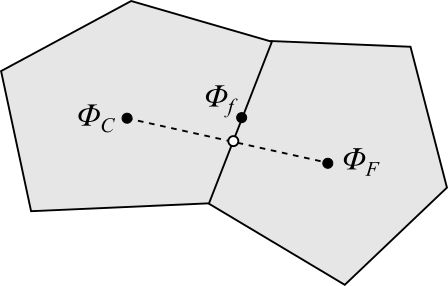
この場合は、面の値を何らかの方法で補正する必要があります(詳細は文献[1])。
節点の値から求める
もう一つの方法は、面を構成する節点(ノード)の値から面の値を求める方法です。
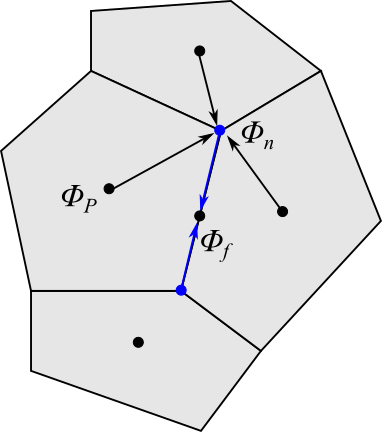
節点の値は、その節点を含むセルの値を用いて、セル中心から節点までの距離で重み付け平均して求めます。
$$\phi_n = \frac{\sum_P (\phi_P / |{\bf x}_n - {\bf x}_P|)}{\sum_P (1 / |{\bf x}_n - {\bf x}_P|)} \tag{7}$$
さらに、節点の値から、距離で重み付けして面中心での値
$$\phi_f = \frac{\sum_n (\phi_n / |{\bf x}_f - {\bf x}_n|)}{\sum_n (1 / |{\bf x}_f - {\bf x}_n|)} \tag{8}$$
を求めます。もしくは、単純に個数平均で、
$$\phi_f = \frac{1}{N} \sum_n \phi_n \tag{9}$$
$N$:節点の個数
で計算することもできます。
確認計算
ここで簡単な確認計算をしてみます。(6)式と(5)式を使って1次元のセルの勾配を求めます。
次のような値を持つセルを考えます。
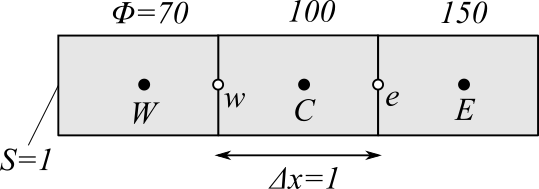
(6)式より$\phi_e$、$\phi_w$の値は、
となります。よって、(5)式より、
$$\begin{split} \nabla \phi_C &= \frac{1}{V_C} (\phi_e {\bf S}_e + \phi_w {\bf S}_w) \\ &= 125 - 85 = 40 \end{split} \tag{13}$$
と、勾配が求まります。
一方、(1)式より、
$$\begin{split} \nabla \phi_C &= \frac{\phi_E - \phi_W}{x_E - x_W} \\ &= \frac{150 - 70}{2} = 40 \end{split} \tag{14}$$
となり、(13)式の勾配と一致することが分かります。
まとめ
今回は、Green-Gaussの定理にもとづく勾配の計算方法について説明しました。ここでは基本的な概略を述べましたが、ソルバーによっては、勾配の値に制限を設けたり、セルの歪みの補正を行ったりと、いろいろなオプションやチューニングをしている場合があります。
あと、勾配計算には最小二乗法を用いた方法もありますが、これは以下の記事で解説しています。