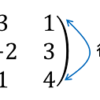以前、QR法で行列の固有値を求める方法について解説しました。
行列の固有値が求まると、それに対応する固有ベクトルが必要になることがほとんどです。今回は固有ベクトルを逆反復法で求める方法についてお話します。
目次
べき乗法
逆反復法に入る前に、そのもととなっているべき乗法について説明しておきます。
べき乗法(power method)とは行列の最大固有値とその固有ベクトルを求める方法です。
$${\bf A}{\bf x} = \lambda {\bf x} \qquad ({\bf x} \neq {\bf 0}) \tag{1}$$
において、
$${\bf x}^{(k)} = {\bf A}{\bf x}^{(k-1)} \tag{2}$$
を繰り返し計算すると、${\bf x}^{(k)}$は行列${\bf A}$の固有値のうち、大きさが最大となる固有値の固有ベクトルに収束します。
また、その時の固有値は
$$R({\bf x}) = \frac{{\bf x}^{\rm T} {\bf A}{\bf x}}{{\bf x}^{\rm T} {\bf x}} = \lambda \tag{3}$$
によって求まります。$R({\bf x})$はレイリー商(Rayleigh quotient)と呼ばれています。このようにして最大の固有値とその固有ベクトルを求める方法がべき乗法です。
ここで、(1)式を変形し、
$${\bf A}^{-1}{\bf x} = \frac{1}{\lambda} {\bf x} \tag{4}$$
とします。
この式に、同様にべき乗法を適用します。(2)式と同様に、
$${\bf x}^{(k)} = {\bf A}^{-1}{\bf x}^{(k-1)} \tag{5}$$
を繰り返し計算すると、行列${\bf A}^{-1}$の最大固有値と固有ベクトルが求まります。ここで、$1/\lambda$の最大が求まるということは、もとの行列${\bf A}$の最小の固有値$\lambda$が求まるということになります。これを逆べき乗法といいます。
逆反復法
今、QR法などで行列の固有値が得られたとします。ただし、この固有値は反復法により求めたため近似値で、真の値とは少し異なります。この近似固有値を$\hat{\lambda}$とします。ここで真の固有値$\lambda$は(1)式を満たします。
そこで、近似固有値$\hat{\lambda}$を使って(1)式を変形すると、
$$({\bf A}-\hat{\lambda}{\bf I}){\bf x} = (\lambda -\hat{\lambda}) {\bf x} \tag{6}$$
と書けます。この式を(4)式のように変形すると、
$$({\bf A}-\hat{\lambda}{\bf I})^{-1}{\bf x} = \frac{1}{\lambda -\hat{\lambda}} {\bf x} \tag{7}$$
となります。これを上述の逆べき乗法で解くと、$\lambda -\hat{\lambda}$の大きさが最小となる固有値とその時の固有ベクトルが求まります。
近似固有値$\hat{\lambda}$が他のどの固有値$\lambda'$よりも真の固有値$\lambda$に近ければ、
$$|\lambda -\hat{\lambda}|<|\lambda' -\hat{\lambda}| \tag{8}$$
となるはずで、$\lambda-\hat{\lambda}$の大きさは最小となっています。
この時の固有ベクトルは(5)式と同様に
$${\bf x}^{(k)} = ({\bf A}-\hat{\lambda}{\bf I})^{-1}{\bf x}^{(k-1)} \tag{9}$$
を繰り返し解くと求まります。しかし、逆行列を求めるのは大変なので代わりに
$$ ({\bf A}-\hat{\lambda}{\bf I}){\bf x}^{(k)} = {\bf x}^{(k-1)} \tag{10}$$
の線形方程式を解いて、${\bf x}^{(k)}$を求めてやります。線形方程式はLU分解などを用いて解くことができます。
つまり、(10)式を繰り返し解くことにより、固有ベクトルを求める方法が逆反復法(inverse iteration method)です。
逆反復法のプログラム
Pythonで逆反復法のプログラムを作成してみます。
import numpy as np
#LU decomposition with partial pivoting- right-looking algorithm
def lu_decomposition(b):
a = b.copy()
n = a.shape[0]
p = np.zeros(n, dtype=int)
for i in range(n):
p[i] = i
for k in range(n-1):
pivot = k
amax = abs(a[pivot][k])
for i in range(k+1, n):
if abs(a[i][k]) > amax:
pivot = i
amax = abs(a[pivot][k])
if pivot != k:
for i in range(n):
tmp = a[k][i]
a[k][i] = a[pivot][i]
a[pivot][i] = tmp
tmp = p[k]
p[k] = p[pivot]
p[pivot] = tmp
for i in range(k+1, n):
a[i][k] /= a[k][k]
for j in range(k+1, n):
a[i][j] -= a[i][k] * a[k][j]
return a, p
# linear solver with LU decomposition
def solve_lu(a, p, y):
n = a.shape[0]
x = np.zeros(n)
#LUx=Py -> x
#Py
for i in range(n):
x[i] = y[p[i]]
#Lz=Py
for i in range(1, n):
for j in range(i):
x[i] -= a[i][j] * x[j]
#Ux=z
for i in range(n-1, -1, -1):
for j in range(i+1, n):
x[i] -= a[i][j] * x[j]
x[i] /= a[i][i]
return x
# input parameter
iter_max = 1000
eps = 1.0e-12
SMALL = 1.0e-6
a0 = np.array([[6., -3., 5.], [-1., 4., -5.], [-3., 3., -4.]])
eigen_value = np.array([3., 2., 1.])
n = a0.shape[0]
eigen_vector = np.zeros((n, n))
for k in range(n):
# A-mu*I
a = a0.copy()
mu = eigen_value[k] + SMALL
for i in range(n):
a[i][i] -= mu
# initial eigenvector
x = np.ones(n)
# LU decomposition
lu, p = lu_decomposition(a)
# inverse iteration method
for iter in range(iter_max):
# linear solver
xold = x.copy()
x = solve_lu(lu, p, xold)
# normalize
norm = np.linalg.norm(x)
for i in range(n):
x[i] /= norm
# convergence check
conv = True
for i in range(n):
err = np.abs(x[i]) - np.abs(xold[i])
if np.abs(err) > eps:
conv = False
break
if conv:
break
# eigen vector
for i in range(n):
eigen_vector[k][i] = x[i]
print("A =\n", a0, "\n")
for i in range(n):
print("Eigenvalue =", eigen_value[i])
print("Eigenvector =", eigen_vector[i], "\n")以下、詳しく説明していきます。
プログラムの冒頭に2つの関数を定義しています。
#LU decomposition with partial pivoting- right-looking algorithm
def lu_decomposition(b):
# linear solver with LU decomposition
def solve_lu(a, p, y):lu_decompositionは行列のLU分解(ピボット付)をして、LU行列と置換ベクトルを返します。
solve_luはLU行列を元に線形方程式を解くソルバーです。
この2つは以下のページで詳しく解説しているので参照してください。
# input parameter
iter_max = 1000
eps = 1.0e-12
SMALL = 1.0e-6
a0 = np.array([[6., -3., 5.], [-1., 4., -5.], [-3., 3., -4.]])
eigen_value = np.array([3., 2., 1.])
n = a0.shape[0]
eigen_vector = np.zeros((n, n))ここは計算のパラメータ入力です。iter_maxは逆反復法の繰り返しの最大数、epsは収束判定値、SMALLは後で説明します。
a0は入力する行列、eigen_valueは固有値(ここでは行列の次数と同じ数の配列としている)、nは行列の次数、eigen_vectorは計算した固有ベクトルを格納する配列(n×nの配列)です。
for k in range(n):
# A-mu*I
a = a0.copy()
mu = eigen_value[k] + SMALL
for i in range(n):
a[i][i] -= mu最初のforループは固有値の数だけ計算するためです。
次に${\bf A}-\hat{\lambda}{\bf I}$を求めます。ここで、近似固有値eigen_valueが真の値と一致すると収束しないことがあるので、微小な値SMALLを加えてずらしています。
# initial eigenvector
x = np.ones(n)
# LU decomposition
lu, p = lu_decomposition(a)固有ベクトルxを初期化します。全て、ゼロだとよくないので、とりあえず1を入れています。
次にLU分解をします。luはLU行列、pは置換ベクトルが返ってきます。
# inverse iteration method
for iter in range(iter_max):
# linear solver
xold = x.copy()
x = solve_lu(lu, p, xold) forループは逆反復法の繰り返し部分です。
前ステップのxをxoldにコピーしてから、solve_lu関数で線形方程式を解いて次のxを求めます((10)式)。
# normalize
norm = np.linalg.norm(x)
for i in range(n):
x[i] /= norm固有ベクトルは定数倍したものも固有ベクトルになります。そこでベクトルの大きさが1になるように規格化してやります。
# convergence check
conv = True
for i in range(n):
err = np.abs(x[i]) - np.abs(xold[i])
if np.abs(err) > eps:
conv = False
break
if conv:
break逆反復法の収束判定部分です。収束判定はいろいろ方法がありますが、ここでは固有ベクトルxのすべての要素の値が、前ステップxoldに比べ変化しなくなったら収束とみなし、繰り返し計算から抜けるようにしています。固有ベクトルは計算中に符号が反転する場合があるので、絶対値をとって判定しています。
# eigen vector
for i in range(n):
eigen_vector[k][i] = x[i]最後にeigen_vectorに固有ベクトルxを格納します。
プログラムでは最終的に、元の行列と固有値、固有ベクトルを出力しています。
プログラムを実行すると、次のように出力されます。
A =
[[ 6. -3. 5.]
[-1. 4. -5.]
[-3. 3. -4.]]
Eigenvalue = 3.0
Eigenvector = [-7.07106781e-01 -7.07106781e-01 5.01098411e-19]
Eigenvalue = 2.0
Eigenvector = [0.30151134 0.90453403 0.30151134]
Eigenvalue = 1.0
Eigenvector = [ 5.58793658e-16 -8.57492926e-01 -5.14495755e-01]上述したように固有ベクトルは定数倍しても固有ベクトルとなるので、最終的な固有ベクトルをさらに規格化することもあります。
ちなみに、この行列の場合、固有値 3, 2, 1に対応する固有ベクトルはそれぞ
固有値:3 → 固有ベクトル:(1, 1, 0)
固有値:2 → 固有ベクトル:(1, 3, 1)
固有値:1 → 固有ベクトル:(0, 5, 3)
なので、数値誤差とそれぞれの定数倍を加味すれば、固有ベクトルが求まっていることがわかります。
まとめ
今回は行列の固有ベクトルを求める方法の一つである逆反復法についてお話しました。
なお、以下のページでは実際に行列の固有値、固有ベクトルを計算できるので、試してみてください。