オンライン熱解析CATTHMの理論式を説明します。
目次
熱回路網法
CATTHMでは熱回路網法に基づいた定式化で計算を行っています。
熱回路網法とは、熱伝達経路を電気回路のアナロジーで構築し計算する手法です。
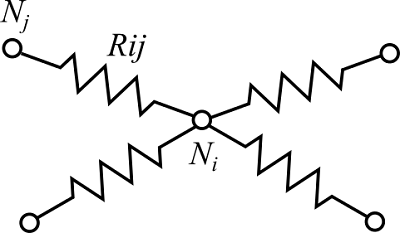
あるノード$N_i$の温度$T_i$は、そのノードに接続する全てのノード$N_j$からの熱流量により決定します。ノード間の熱抵抗を$R_{ij}$とすると、以下の式が成り立ちます。
$$C_i \frac{d T_i}{d t} = \sum_j \frac{T_j - T_i}{R_{ij}}+Q_i$$
ここで、$C_i$:ノード$N_i$の熱容量、$t$:時間、$Q_i$:ノード$N_i$の発熱量。
これはキルヒホッフの法則と呼ばれています。
時間変化がない定常状態であれば、左辺はゼロとなるため、ノードに出入りする全ての熱流量の総和はゼロとなり、つり合っています。
熱抵抗
熱伝達には、伝導、対流、放射などの熱伝達様式がありますが、それぞれについて熱抵抗が定義できます。
詳細は以下のページを参照してください。
流体抵抗網法
流体ながれは、流体抵抗網法で計算しています。流体抵抗網法は、熱回路網法と同様に、流体経路を流体抵抗を用いて定式化します。
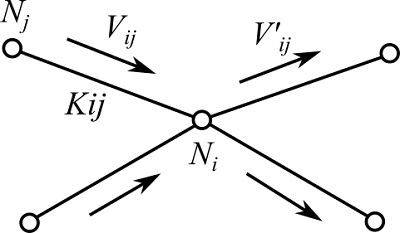
流体ノード$N_i$に流入する流量を$V$、ノードから流出する流量を$V'$とすると、流量のつり合いから、以下の式が成り立ちます。
$$\sum_j V_{ij} = \sum_j V'_{ij}$$
また、ノードの圧力を$P_i$、ノード間の流体抵抗係数を$K_{ij}$とすると、
$$P_j - P_i = K_{ij} \frac{\rho u_{ij}^2}{2}$$
ここで、$u_{ij}$:流速($=V_{ij}/A$)、$A$:断面積
が成り立ちます。これより、流量$V_{ij}$は、
$$V_{ij} =\sqrt{\frac{2A^2}{\rho} \frac{P_j - P_i}{K_{ij}}}$$
と書けます。
これらの式から圧力を求め、各流体経路を流れる流量を計算します。
直管の抵抗係数
CATTHMでは、抵抗係数を指定しない場合、直管の管摩擦による流体抵抗で計算します。
直管の抵抗係数$K$は、ダルシー=ワイスバッハの式(Darcy-Weisbach formula)より、
$$K = \lambda \frac{l}{d}$$
ここで、$\lambda$:管摩擦係数、$l$:管の長さ、$d$:管の直径
と表されます。
管摩擦係数は、層流で$\lambda=64/Re$、乱流で$\lambda=0.3164 Re^{-0.25}$(ブラジウスの式)で計算しています。ここで、レイノルズ数 $Re=\rho u d / \mu$。
流路内の熱移動
流体回路のノード$N_i$に対する熱移動は、流体の移流によって運ばれる熱と、熱回路から伝達する熱のつり合いにより、以下の式が成り立ちます。
$$\sum_j \rho Cp V_{ij} T_j + q_i = \sum_j \rho Cp V'_{ij} T_i$$
ここで、$\rho$:流体密度、$Cp$:流体の比熱、$q$:熱回路より流入する熱量。
熱回路モデルとこの式を連成することで、すべてのノードの温度が求まります。
※非定常計算における流体回路の熱容量は、そのノードに接続する管の半分の体積の積算値から計算しています。
数値解法
定常計算は、双共役勾配法による反復法で解を求めています。非定常計算は、Runge-Kutta-Fehlberg法により、時間刻みを自動で制御して計算しています。
