的あてゲーム（ボールの軌跡計算）

ボールを的に当てるゲーム

コーヒーブレイクのための簡単なゲームです。

初速と角度を調整して、100mはなれた的にボールを当ててください。空気抵抗と回転を考慮した運動方程式を解いているので、球の軌跡を把握するシミュレーションに使えます。

遊び方

条件を入力して、[計算実行]ボタンを押すとボールの軌跡が計算されます。[初速]と[射出角度]を調整して、100mはなれた赤い的に当ててください。
[球の種類]でボールの種類を選択できます。[球の直径]と[球の質量]が入力されます。
[球の回転数]で回転数を設定します。トップスピン（順回転）はプラス、バックスピン（逆回転）はマイナスの数値で入力してください。
[空気抵抗]のチェックをはずすと、空気抵抗を考慮しない計算になります。
[風速変更]ボタンを押すと、ランダムに風速が変更されます。マイナスは向かい風です。
[クリア]ボタンで、表示がクリアされます。
条件の数値は直接変更できます。

計算手法

球の軌跡は空気抵抗および球の回転を考慮した運動方程式を解いています。

運動方程式

球の運動方程式は次式で与えられます。

$$ m \frac{d \vec{v_p}}{d t} = \vec{F_d} + \vec{F_l} + \vec{F_g} $$

$m$：球の質量、$\vec{v_p}$：球の速度、$t$：時間、$\vec{F_d}$：抗力、$\vec{F_l}$：揚力、$\vec{F_g}$：重力

抗力

球にかかる抗力（空気抵抗）は次式で与えています。

$$\vec{F_d} = \frac{1}{2} C_d \rho A |\vec{V} |\vec{V} $$

$\vec{V} = \vec{v_f}-\vec{v_p}$ ：風速と球の速度の相対速度、$\vec{v_f}$ ：風速、$C_d$：抗力係数、$\rho$：空気の密度、$A= \pi r^2$：球の投影面積、$r$：球の半径

$C_d$ は球の抗力係数とし、以下のページにあるMorrisonの式[1]を使っています。

なお、風速は高度によらず一様で、地面に水平に吹いているものとしています。実際のボールは表面状態や回転の影響で、空気抵抗が理想的な球とは異なるため、飛距離が違ってくるかも知れません。

揚力

回転する球にはマグヌス力による揚力がかかります。マグヌス力は以下の式で与えています。

$$\vec{F_l} = \frac{1}{2} C_l \rho A |\vec{V} |^2 \frac{\vec{V} \times \vec{\omega}}{|\vec{V} \times \vec{\omega}|}$$

$C_l$：揚力係数、$\vec{\omega}$：球の回転の角速度ベクトル

揚力は球の進行方向（風がある場合は風と球との相対速度の方向）に対して垂直方向に作用します。

揚力係数 $C_l$ はレイノルズ数 $Re$ やスピンパラメータ $S = r \omega / |\vec{V} |$（球の進行速度と回転速度との比）の関数になります。一般的に実測により $C_l$ を求めますが、ここでは $C_l$ は $S$ のみに依存するとして、以下の２つの形式により与えています。

・線形[2]

$C_l$ はスピンパラメータに比例すると仮定します（$k_l$は比例係数）。

$$C_l = k_l S$$

・Maccollの測定値[3]

Maccollによる滑らかな球の実測値から $C_l$ を与えます。

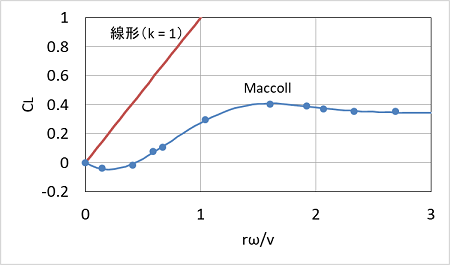
$C_l$の与え方は以下で設定できます。

また、球の回転は空気との摩擦により減衰します。回転の減衰は、以下の式により計算しています。

$$ I \frac{d \vec{\omega}}{dt} = \vec{M}$$

$$\vec{M} = -\frac{1}{2} C_m \rho A |\vec{V} |^2 d \frac{\vec{\omega}}{|\vec{\omega}|}$$

$I=(2/5)mr^2$：球の慣性モーメント、$\vec{M}$：空力回転減衰トルク、$C_m$：空力回転減衰係数、$d$：球の直径

$C_m$はレイノルズ数 $Re$ やスピンパラメータ $S$ の関数になっていると考えられますが、ここではゴルフボールの実測結果[4]を参考に、単純な仮定としてスピンパラメータに比例するとしています。この文献から、デフォルトの比例係数を0.01としています。

$$C_m = k_m S$$

係数は以下で変更できます。実際はボールの種類や表面形状などにより回転減衰係数は変わると思われるので、あくまで簡易的なモデルです。

重力

球には以下の重力がかかります。$\vec{g}$ は重力加速度ベクトル。

$$\vec{F_g} = m \vec{g}$$

数値解法

運動方程式は４次のRunge–Kutta法で解いています。

参考文献

[1] Morrison, F. A. An Introduction to Fluid Mechanics, Cambridge University Press, New York, 2013

[2] Leroy, W. A. Aerodynamics of the Curve-Ball: An Investigation of the
Effects of Angular Velocity on Baseball Trajectories. https://www.researchgate.net/publication/241376252

[3] Maccoll, J. W. Aerodynamics of a Spinning Sphere. The Journal of the Royal Aeronautical Society. 1928, vol. 28, p. 777-798.

[4] 溝田武人ら. 風洞実験用空気静圧軸受型4 分力ロードセルの開発研究. 日本風工学会論文集, 2016, vol. 41, no. 2 (no. 147), p. 48-57

球の種類		初速 $v_p$ [m/s]
球の直径 $d$ [m]		射出角度 $\theta$ [deg]
球の質量 $m$ [kg]		球の回転数 $s$ [回転/s]
空気抵抗		風速 $v_f$ [m/s]