目次
球の抗力係数
球の抗力係数を計算します。球の直径、流体密度、粘性係数、速度を入力して、算出式を選択してください。レイノルズ数、球の抗力係数、抗力が算出されます。※デフォルトの流体物性は、20℃の空気の物性値です。
スポンサーリンク
計算式
球の抗力係数$Cd$は、レイノルズ数$Re$により変化し、$Re$が$10^{3}$までは減少し、$Re$が$10^{3}$～$10^{5}$では0.4程度で一定となり、$Re \sim 3 \times 10^{5}$の臨界レイノルズ数に達すると、境界層は乱流に遷移し、その後乱流はく離して0.1以下に減少します。
球の抗力係数$Cd$を近似する式は各種提唱されていますが、ここでは次の2つの近似式で計算しています。Clift and Grauvinの式は、臨界レイノルズ数以下で扱われます。Morrisonの式は、臨界レイノルズ数からの急な減少も考慮しており、より広範囲にわたり近似できています。
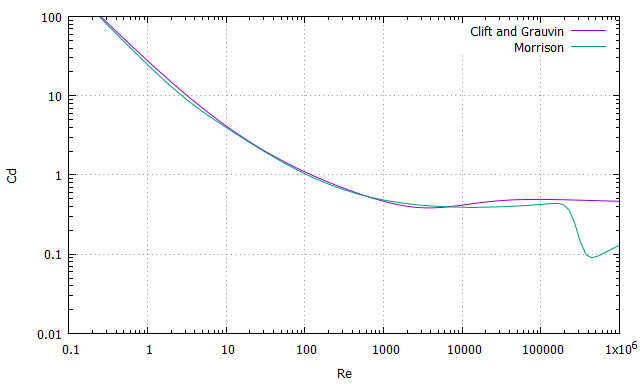
Clift and Grauvinの式
$Re < 3 \times 10^{5}$
$$Cd = \frac{24}{Re}(1+0.15 Re^{0.687}) + \frac{0.42}{1+4.25 \times 10^{4} Re^{-1.16}}$$
$Re = \rho u d / \mu$：レイノルズ数、$\rho$：流体密度、$u$：速度（球と周囲流体との相対速度）、$d$：球の直径、$\mu$：粘性係数
Ref : Clift, R. and Grauvin, W. H. (1970) Proc. Chemeca '70, 1 , 14
Morrisonの式
$$Cd = \frac{24}{Re} + \frac{2.6 (Re/5.0)}{1+(Re/5.0)^{1.52}}
+\frac{0.411(Re/(2.63 \times 10^{5}))^{-7.94}}{1+(Re/(2.63 \times 10^{5}))^{-8.0}}+\frac{0.25(Re/10^{6})}{1+(Re/10^{6})}$$
Ref：Morrison, F. A. (2013) An Introduction to Fluid Mechanics, Cambridge University Press, New York
球の抗力
球の抗力$F$は以下の式で求まります。
$$F = \frac{1}{2} C_{d} \rho A u^{2}$$
$A=\pi d^2/4$：球の投影面積