今回は流体解析などで使われる残差と収束判定についてお話します。
目次
残差とは
有限体積法の流体解析をされる方は、残差という言葉を聞いたことがあると思います。「残差が大きい」とか「残差が下がらず収束しない」など、よく使われます。
「残差は真の解からの差のことである」と思っている方が意外と多いですが、これは違います。そもそも真の解が解析的に分かれば流体解析で計算をする必要がないわけで、真の解というのが不明だからこそ数値計算をするのです。
流体計算でメッシュを作成して境界条件を与えると、その系を表す流体方程式から線形方程式(連立方程式)が作られます。詳しくは以下の記事を参照してください。
線形方程式は係数行列${\bf A}$、未知数ベクトル${\bf x}$、定数項ベクトル${\bf b}$とすると、
$${\bf A}{\bf x}={\bf b} \tag{1}$$
と表すことができます。もし、${\bf x}$がこの方程式系を完全に満たす解であれば、(1)式の右辺から左辺を引くとゼロになるはずです。しかし、この方程式を前述の記事にある共役勾配法のような反復解法で解くと、${\bf x}$が完全には方程式を満たさず、
$${\bf R}={\bf b}-{\bf A}{\bf x} \tag{2}$$
のように、左辺と右辺に差${\bf R}$が生じています。これを残差といいます。つまり、残差というのは「その解がどれだけ元の方程式を満たしているか」という指標になります。
反復法で計算ステップが進むにつれ、解${\bf x}$が方程式を満たしてくると、残差は小さくなって行きます。この時、「計算が収束してくる」といいます。逆に、残差が大きくなって、解が方程式を全く満たさなくなれば、「計算が発散する」といわれます。
絶対残差
今、(2)式を少し書き換えて各セル${C}$ごとの残差$R_C$を考えます。
${F}$は隣接セルを表しており、大きさだけを考えるように絶対値をとっておきます。(3)式は絶対残差と呼ばれます。
反復解法で理想的には、解${\bf x}$が方程式を完全に満たし残差がゼロになると、完全に収束し解が求まった状態になります。しかし、さまざまな数値誤差や解法やアルゴリズムの違いにより、残差が完全にゼロになることはありません。そこで、通常はどこかで計算を打ち切る必要があります。残差はこの収束判定に使われています。
例えば(3)式はセルごとの残差ですが、全体のセルの中で一番大きな残差の値がある閾値より小さければ収束とみなすといった具合です。
ここで、$\max$はセル全体のなかでの最大値、$\varepsilon$は収束判定の閾値(収束判定値)です。
ここで、一つ注意することがあります。例えば具体的な数値で考えてみます。
いま、2つの異なる系があったとします。一つは、①$b_C$ = 1000、$a_C$ = 1、$x_C$ = 999(Fの項は考えないものとします)。もう一つは、②$b_C$ = 0.2、$a_C$ = 1、$x_C$ = 0.1の値を持っていたとします。
この時の絶対残差は、①で$R_C$ = 1、②で$R_C$ = 0.1となります。
さて、②の方が残差が小さいので、②の方が収束していると言えるでしょうか?
これは違いますね。①では解$x_C$ = 1000、②では$x_C$ = 0.2が本当の解であるため、①は相対的な誤差で言えば0.1%、②は50%となり、①の方がより真の解に近いということが言えます。
つまり、絶対残差の指標は、結果の値の大小が異なる条件では比較することが難しいのです。
相対残差
そこで、絶対残差を何かの値で割って規格化した相対残差を考えます。
$$R_C = \frac{ \left| b_C - \left(a_C x_C + \sum a_F x_F \right) \right| }{M_C} \tag{5}$$
ここで、${M_C}$は規格化係数です。
${M_C}$をどうするかはさまざまです。例えば$a_C x_C$もしくは$b_C$の最大値
$$M_C = \max |a_C x_C| \tag{6}$$
$$M_C = \max |b_C| \tag{7}$$
で規格化するというのが考えられます。全体の収束判定は(4)式と同様に、全セルのうち(5)式の残差の最大が収束判定値$\varepsilon$より小さければ収束とみなすということにします。
こうすると、計算される残差は相対的な値になり、解の大きさが異なっても比較することができるようになります。
さまざまな残差の定義
収束判定に使われる残差の式は実にさまざまなものがあります。上記にあげたのはあくまで一例にすぎません。他には例えば、系全体の残差を二乗和の平方根の形で表したものや
ノルムの和で表したもの
なども使われます。
また、規格化係数も物理量によっては、系に流入するフラックスの大きさを係数として与えるという場合もあります。他にも考えられますが、いずれにしても残差の定義はいろいろあるということです。
ちなみに当サイトのオンライン流体解析ツールCATCFDzeroは(9)式をベースにした残差で収束判定を行っています。
解析ソフトによる違い
流体解析ソフトウェアで出力される残差は、使うソフトによってその定義は異なっています。残差の定義が違うと、残差の大きさも異なります。つまり、あるソフトと別のソフトの残差はそのまま同列で比較することはできません。
筆者は以前とある商用流体解析ソフトの責任者をしていたことがありますが、そのソフトの後継となる別のソフトを売り出した際の出来事です。後継ソフトは一から作った新しいソフトのため、残差の定義も全く異なったものでした。後継ソフトの残差は、先発ソフトに比べ少し大きめに計算される傾向にありました。先発ソフトに慣れたお客様からは、後継ソフトは収束性が悪いとかなりクレームを頂き、定義式の違いによる残差の大きさの違いを説明するのに苦労した記憶があります。
要するに定義式が違うプログラム同士を比較する際には注意が必要だということを理解しておくことが大事です。
収束判定の指標
解析ソフトにより残差の定義は異なるものの、一般的には収束判定値$\varepsilon$は、おおよそ10-3~10-5程度に設定されていることが多いと思います。
定常計算では通常は、ソフトのデフォルトの収束判定値を満たせば計算を終える、という場合が多いと思いますが、これも実は注意が必要です。
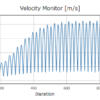
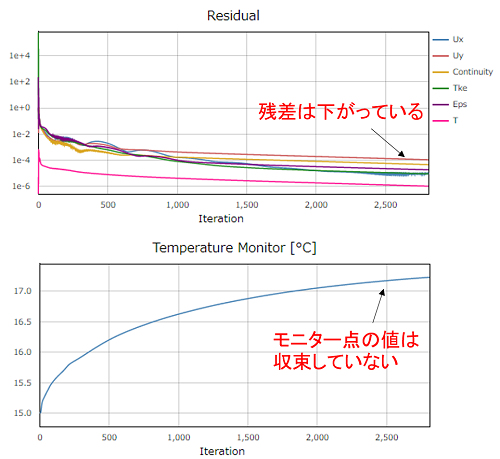
残差が結構下がっているにも関わらず実際には収束していなくて、計算ステップ間で解が変動していることが結構あります。
そこで、収束判定は残差だけでなく他の指標を合わせて行うようにした方がよいです。
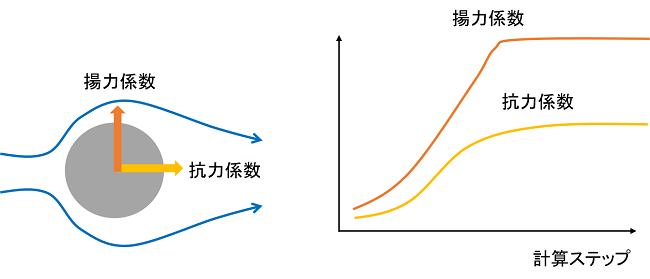
例えば外部流れの空力計算であれば、物体にかかる抗力係数や揚力係数の値を一緒に出力し、計算ステップが進むにつれてそれらの係数がどのように変動しているかを見る必要があります。残差は下がっても、それらの値がまだ一定になっていないということがよくあるからです。
熱であれば、物体や境界の熱量や温度をモニターしそれらが一定になって収束しているか見るのも重要です。また、最低限どこか着目したい位置での速度や温度などの値の収束状況は毎回確認した方がよいと思います。着目したモニター値がまだ収束していない場合は、残差の収束判定値を小さくしてさらに計算を続けるようにします。
また逆に、メッシュや条件が厳しく残差が下がりきらない場合でも、着目しているモニターの値が収束していれば、計算を打ち切るということもしばしばあります。
いずれにしても残差だけに頼らず、他の指標を合わせて見ていくとよいでしょう。
計算が収束しない場合の対処は、以下の記事もご参考ください。
内部反復と外部反復
最後に少しややこしい話ですが、有限体積法による流体解析のアルゴリズムは内部反復と外部反復に分けられます。非圧縮性流体の解法でよく使われるSIMPLE法は反復解法ですが、一般的に計算ステップとか収束判定、残差というのは、このSIMPLE法(もしくはそれに準ずるアルゴリズム)に関わるものとして出てきます。「定常計算で300ステップで収束して残差は10-4まで下がった」とか言いますね。
ところが、このSIMPLE法の1ステップの中でも運動量や温度、圧力などでそれぞれ行列が解かれます。この行列解法には共役勾配法などが使われますが、この解法も反復解法です。SIMPLE法の各ステップの反復を外部反復、その1ステップ中の行列解法の反復を内部反復と呼んだりしています。
※呼び方は解析ソフトにより様々で、内部反復は非定常計算アルゴリズムの補正ループを指す場合もあります。
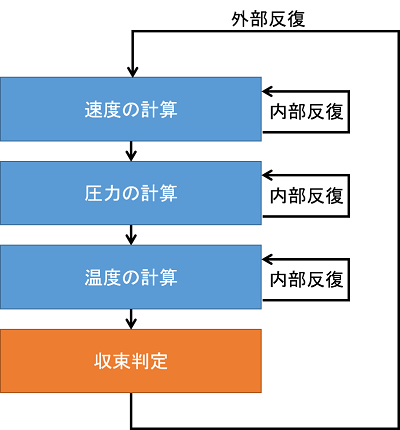
前述のように通常、計算ステップとか残差とか収束判定という場合、この外部反復の方を指します。
しかし、外部反復も内部反復もどちらも反復法なので、実際にはそれぞれで残差が定義され収束判定が行われます。解析ソフトでは、この外部と内部の収束判定値を別々に与えることができるようになっています。通常は外部反復の収束判定しか意識していないと思いますが、内部の反復計算も行われているので、出力結果や設定などをよく見てみてください。
まとめ
今回は、残差と収束判定についてお話しました。ソフトウェアを使った解析では残差の定義式まで確認することは通常はないと思いますが、自分が計算している式がどのようになっているか知っておくことは、計算結果を評価するうえでも重要になることがあります。