今回は疎行列の計算においてデータを効率的に扱うことができる圧縮行格納方式(Compressed Row Storage)という手法についてお話します。
疎行列とは
疎行列(sparse matrix)とは、その要素のうちほとんどがゼロである行列をいいます。以前、有限体積法の講座のときに出てきたので、そちらも参照してください。
流体解析などの数値計算で方程式を作る場合、たとえ100万個のセルがあったとしても、一つのセルの方程式は自分自身のセルと隣合う数個のセルのみでたてられます。つまり、その方程式系から作られる100万×100万の行列を見ると、1行あたり高々数個程度の要素のみが非ゼロで、他は全てゼロという行列になります。これが疎行列です。
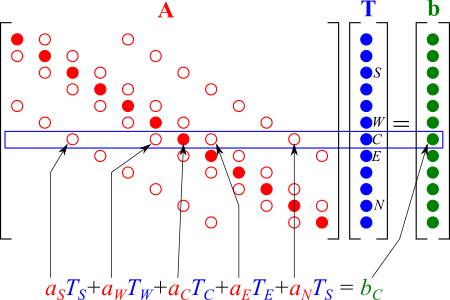
A行列で●○以外は全てゼロ
このような行列の計算をプログラミングするときに、多くのN個のセルから作られるN×N個の要素を持つ配列を宣言すると莫大なメモリが必要になり、メモリの確保すら出来なくなるという状態になります。しかも、そのほとんどの要素はゼロで要素同士の演算において全く寄与しないため、メモリも計算量も無駄になってしまいます。
圧縮行格納方式(Compressed Row Storage)
そこで、このような大規模な疎行列のデータを効率よく格納する方法として、圧縮行格納方式(Compressed Row Storage : CRS)という方法が考えられています。
CRSのコンセプトは非ゼロの要素のみをデータとして持たせることにより行列全体を圧縮することです。例えば、1000×1000(=100万)個の行列要素も、たかだか数1000個の要素に圧縮することができます。
では、具体的なCRSの方法を見ていきましょう。まず、次のような5×5の疎行列${\bf A}$を考えます。
まずこの行列の非ゼロの成分を一番上の行から順番に配列aに格納していきます。
| a | 3 | 7 | 9 | 2 | 1 | 4 | 6 | -5 | -1 | -8 | 7 | 6 |
|---|
次にそれぞれの要素が一行のうち何列目の要素かを配列colに格納します。ここで、列番号は0から始まるとしましょう。
| col | 0 | 2 | 4 | 2 | 3 | 0 | 1 | 2 | 2 | 3 | 1 | 4 |
|---|
そして、各行の最初の非ゼロの要素が配列aの何番目の要素かを配列rowに格納します。順番は0番から始めます。rowは行列の(行数+1)個の要素を持ち、最後の要素には配列aの要素数を入れておきます。
| row | 0 | 3 | 5 | 8 | 10 | 12 |
|---|
これでデータの準備ができました。
では、行列${\bf A}$とベクトル${\bf x}$の積${\bf A}{\bf x}$を計算してみましょう。${\bf x}$は、
とします。CRSを使って行列の積を計算するプログラムをPythonで書いてみます。
n = 5
a = [3, 7, 9, 2, 1, 4, 6, -5, -1, -8, 7, 6]
col = [0, 2, 4, 2, 3, 0, 1, 2, 2, 3, 1, 4]
row = [0, 3, 5, 8, 10, 12]
x = [2, 5, -3, 8, 4]
b = [0, 0, 0, 0, 0]
# A*x
for i in range(n):
b[i] = 0
for j in range(row[i], row[i+1]):
b[i] += a[j] * x[col[j]]
print(b) 積${\bf A}{\bf x}$を配列bに計算します。まず最初のfor文で行列の行数分ループします。次のforループでrow[i]からrow[i+1]までインデックスjで回します(jにはrow[i+1]は含みません)。row配列には各行の非ゼロ要素がa配列の何番目から始まるかが格納されています。つまりa[j]でその行での非ゼロ要素を取得することができます。また、col[j]はその要素の列番号を返すので、x[col[j]]でa[j]に対応したx要素をすぐに返すことができます。
実行すると配列bが次のように出力されます。
[21, 2, 53, -61, 59]
このようにCRS法では非ゼロ要素のみを格納したデータから行列の計算を行うことができます。
なお、流体解析などで使う行列解法では行列の対角成分と非対角成分を分けておいた方が扱いやすかったり、上三角行列や下三角行列を取り出したい場合があります。その場合は、それらの成分を分けて格納したり、必要なデータにすぐにアクセスできるように別のインデックスを用意したり工夫するとよいでしょう。
また、CRSの他にもいろいろ別の方法も考えられています。
