前回は有限体積法の境界条件についてお話しました。
今まで数式の導出が続きましたが、いよいよ今回からPythonで有限体積法のプログラムを作っていきたいと思います。まず構造格子のメッシュ情報を取得するプログラムを作ります。
セル番号
今回は2次元の熱伝導を解く問題です。形状は矩形なので、$x$ 方向、$y$ 方向に規則正しく並んだ直交構造格子のメッシュとしましょう。セルの縦横の幅はどれも同じとします。
このメッシュでセルの位置を $x$ 方向は $i$、$y$ 方向は $j$ の文字で表すことにします。これは差分法のときと同じですね。
いま $x$ 方向に $N_x$ 個、$y$方向に $N_y$ 個セルが並んでいるとします。このメッシュ全体のセルの数は $N_x \times N_y$ 個です。$i$ は1から $N_x$、$j$ は1から $N_y$ まで1ずつ増えていきます。

このメッシュでは、$i$ と $j$ を指定するとそのセルの位置、そのセルの中心の座標がすぐに分かります。左下角を原点とすると、セル中心の座標 $(x, y)$ は次式で求まります。
$$ \begin{split} x &= \left(i - \frac{1}{2} \right) \Delta x \\ y &= \left(j - \frac{1}{2} \right) \Delta y \end{split} \tag{6-1}$$
ここでは $i$ と $j$ を使ってセルを特定したのですが、一方でセルを通し番号で整理した方がよい場合があります。あとの方で出てきますが、方程式を数値的に解く場合にベクトルや行列の計算をする必要がありますが、そのときには2次元的な番号ではなく、1次元的な通し番号で扱ったほうが便利です。
このメッシュで、セルの通し番号を左下角を1として $x$ 方向に1ずつ増やして、右端まで行くと 1つ上の段の左端に行くような順番とします。
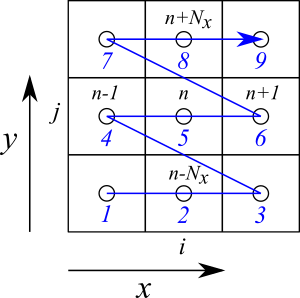
このとき、セル番号 $n$ は $i$、$j$ を用いて次のように表されます。
$$n = i + (j - 1) N_x \tag{6-2}$$
また、これまで導出してきたように有限体積法の計算では、あるセルに隣接する周りのセルの値が必要になります。セル $(i,j)$ に隣接するセルの番号は簡単に求めることができます。
$$ \begin{split} C &: (i, j) \rightarrow n \\ E &: (i+1, j) \rightarrow n+1 \\ W &: (i-1, j) \rightarrow n-1\\ N &: (i, j+1) \rightarrow n+N_x \\ S &: (i, j-1) \rightarrow n-N_x \end{split} \tag{6-3}$$
ただし、境界面に隣接するセルの場合は注意が必要です。例えば、$i=N_x$ すなわち領域の右端のセルはEastの隣接セルはありません。他の端面のセルについても同様です。
Pythonプログラム
ではここまでの情報をPythonでプログラミングしてみましょう。セル $(i,j)$ に対してセル番号と隣接セルの番号を求めるプログラムです。
lx = 0.3
ly = 0.3
nx = 3
ny = 3
dx = lx / nx
dy = ly / ny
ncell = nx * ny
for i in range(1, nx+1):
for j in range(1, ny+1):
icell = i + (j - 1) * nx
x = (i - 0.5) * dx
y = (j - 0.5) * dy
print('i j = ', i, j)
print('icell = ', icell)
print('x y = {:6.3f} {:6.3f}'.format(x, y))
#-- face loop
for iface in range(4):
#-- face type
if iface == 0 and i == nx:
ftype = 'right'
elif iface == 1 and i == 1:
ftype = 'left'
elif iface == 2 and j == ny:
ftype = 'top'
elif iface == 3 and j == 1:
ftype = 'bottom'
else:
ftype = 'internal'
#-- neighbor cell
if ftype == 'internal':
if iface == 0: inbor = icell + 1 # East
elif iface == 1: inbor = icell - 1 # West
elif iface == 2: inbor = icell + nx # North
elif iface == 3: inbor = icell - nx # South
else:
inbor = 0
print('face {:d} {:9s} {:d}'.format(iface, ftype, inbor))
print(' ')まず、lx、ly は $x$方向、$y$方向の領域の長さ、nx、ny はそれぞれの方向のセル数です。ここでは3×3の9個のセルで計算しています。
dx、dy はセルの幅、ncell は全体のセル数を計算しています。
for i in range(1, nx+1):
for j in range(1, ny+1):
icell = i + (j - 1) * nx
x = (i - 0.5) * dx
y = (j - 0.5) * dyここは i、j に対してforループを回しています。i、j は1から始まるので、range(1, nx+1)は1から nx+1 としています。これで1から nx までのループが回ります。nx+1 より一つ小さい整数までです。
icell は(6-2)式を計算していて、$n$ に相当するセル番号です。x、y は(6-1)式で求めています。
for iface in range(4):次のforループはセルの面に対するループです。セルには必ず4面あるので4回ループを回します。iface は面のインデックスで、このプログラムでは 0=East、1=West、2=North、3=South と定義することにします。
if iface == 0 and i == nx:
ftype = 'right'
elif iface == 1 and i == 1:
ftype = 'left'
elif iface == 2 and j == ny:
ftype = 'top'
elif iface == 3 and j == 1:
ftype = 'bottom'
else:
ftype = 'internal'ここは、その面がどういう面かを判定して ftype という変数に面のタイプを返しています。面のタイプは、領域の右端が 'right'、左端が 'left'、上端が 'top'、下端が 'bottom'、それ以外は内部の面で 'internal' という名前をつけています。iface=0(East)で i=nx のときは右端面という具合です。'internal' 以外は境界面となります。
if ftype == 'internal':
if iface == 0: inbor = icell + 1 # East
elif iface == 1: inbor = icell - 1 # West
elif iface == 2: inbor = icell + nx # North
elif iface == 3: inbor = icell - nx # South
else:
inbor = 0 最後に面に隣接するセルのセル番号 inbor を求めています。ftypeが 'internal'(内部の面)のときは(6-3)式からセル番号を求めます。それ以外の境界面では隣接セルがないため、inbor を0としています。
printでそれぞれの情報を書き出すと次のように出力されます。
i j = 1 1
icell = 1
x y = 0.050 0.050
face 0 internal 2
face 1 left 0
face 2 internal 4
face 3 bottom 0
i j = 1 2
icell = 4
x y = 0.050 0.150
face 0 internal 5
face 1 left 0
face 2 internal 7
face 3 internal 1
...これで、全てのセルで4つの面とそれに隣接するセルの番号を取得することができました。構造格子の場合はこのように簡単に周りのセルの情報を得ることができます。
まとめ
今回はPythonでメッシュの情報を取得するプログラムを作成しました。隣接するセルが分かれば、前に説明した $a_C$ や $b_C$ などの係数を計算することができます。次回はこれらの係数を計算するプログラムを作っていきたいと思います。
