前回は離散化と差分法について説明しました。熱伝導方程式を離散化しFTCS法の形式で書くことができました。
今回からいよいよプログラミングに入ります。。。
が、その前に条件を整理しておきたいと思います。
目次
計算モデル
プログラミングに入る前に、どのような計算をしていけばよいか、条件はどのようなものかを整理していきましょう。この過程はとても重要です。これがきちんとできているとプログラム作成もスムーズにできます。
なお、ここでやるように計算条件を整理したものを計算モデルと呼んでいます。
問題
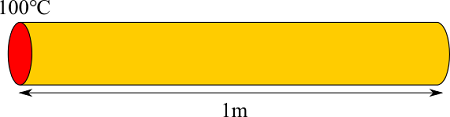
今回解く問題は次のものでした。
方程式
解く方程式は次の熱伝導方程式です。
$$\frac{\partial T}{\partial t} = \alpha \frac{\partial^2 T}{\partial x^2} \tag{1}$$
ここで、$\alpha=\lambda/(\rho C_p)$ は熱拡散率。
数値解法
数値解法はFTCS法を使います。
$$T_i^{n+1} = T_i^n + \Delta t \ \alpha \frac{T_{i+1}^n - 2 T_i^n + T_{i-1}^n}{\Delta x^2} \tag{2}$$
離散化
空間をどのように離散化するかを考えましょう。長い棒なので1次元とします。棒の長さは $L_x = 1 $ m です。この棒を端を含めて $N_x$ 個の点に分割します。したがって、分割した幅は $\Delta x = L_x / (N_x - 1)$ となります。
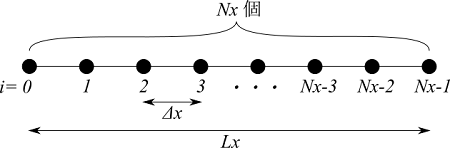
ここで、点に番号をつけておきましょう。左の先端を $i = 0$ とし 1 ずつ増やしていきます。$N_x$ 個あるので、反対の端は $i = N_x - 1$ となります。
分割数ですが、ひとまず $N_x = 101$ としましょう。$\Delta x = 0.01$ m となります。
時間は0秒からはじまり、時間刻み $\Delta t$ ずつ増えて行きます。$\Delta t = 0.1$ 秒でまずは計算してみます。計算期間はちょっと長めに、20,000秒間(約5.6時間)とします。
物性値
(1)式を計算するときに必要な物性値を与えておきます。材料は銅なので物性値は、密度 $\rho = 8880$ kg/m3、熱伝導率 $\lambda = 398$ W/(m K)、比熱 $C_p = 386$ J/(kg K) とします。熱拡散率はプログラム内で計算させましょう。
初期条件
時刻0秒のときの初期条件は、全ての点で温度0℃です。
境界条件
空間分布のある問題を解くときには、一番端がどういう条件になっているかを決めてやる必要があります。これを境界条件といいます。
今回の問題から、一方の端を100℃に熱するとあるので、$i=0$ の点の温度を100℃に固定します($T_0=100$℃)。このように、解きたい量の値を固定する境界条件をディリクレ(Dirichlet)条件といいます。
では反対の端($i=N_x - 1$)はどうすればよいでしょう。問題では熱する先端以外の表面は断熱とあります。断熱とは熱の出入りがないという意味です。熱伝導方程式の導出の回でやったとおり、熱の出入りする量は次式で表せます。
$$Q = - \lambda \frac{\partial T}{\partial x} A \tag{3}$$
熱の出入りがないということは、$Q=0$ となるので(3)式は、
$$\frac{\partial T}{\partial x} = 0 \tag{4}$$
となります。つまり温度勾配が0という条件なのです。これを後退差分を用いて書くと、
$$\frac{T_{Nx-1}-T_{Nx-2}}{\Delta x} = 0\tag{5}$$
となり、結局
$$T_{Nx-1}=T_{Nx-2} \tag{6}$$
であることがわかります。つまり隣の温度と同じというのが断熱の境界条件になります。なお、このように勾配を指定する境界条件をノイマン(Neumann)条件といいます。
結果出力
空間の時間変化を解く問題なのでアニメーションにしたいと思います。第2回シリーズで出力したのと同じようにアニメーションを作成しましょう。
まとめ
ちょっと長くなったので本日はこれで終わりにしたいと思います。プログラミングに入れませんでした。。。
しかし、計算モデルをしっかり整理して、条件などをきちんと考えておくと、プログラミングはとても楽になります。この作業は数値計算プログラミングにおいてとても重要なので、面倒でもしっかりまとめておきましょう。
さて、次回こそPythonでプログラミングしていきます。
