前回は、惑星の運動方程式をルンゲ=クッタ法で解くプログラムを作成しました。
今回は、惑星の運動をアニメーションで表示する処理を追加し、プログラムを完成させたいと思います。
目次
惑星の軌道計算プログラム
早速ですが、今回作る惑星の軌道計算プログラムを載せておきます。
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
# parameter
r = np.array([0.0, 1.0])
v = np.array([-1.0, 0.0])
t = 0.0
dt = 0.001
nt = 10000
nout = 20
# graph data array
gx = []
gy = []
ims = []
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
# function
def fr(v):
return v
def fv(r):
rnorm = np.linalg.norm(r)
return -r / rnorm**3
# time loop
for i in range(nt):
rp = r
vp = v
kr1 = fr(vp)
kv1 = fv(rp)
rp = r + 0.5 * dt * kr1
vp = v + 0.5 * dt * kv1
kr2 = fr(vp)
kv2 = fv(rp)
rp = r + 0.5 * dt * kr2
vp = v + 0.5 * dt * kv2
kr3 = fr(vp)
kv3 = fv(rp)
rp = r + dt * kr3
vp = v + dt * kv3
kr4 = fr(vp)
kv4 = fv(rp)
r += dt * (kr1 + 2.0 * kr2 + 2.0 * kr3 + kr4) / 6.0
v += dt * (kv1 + 2.0 * kv2 + 2.0 * kv3 + kv4) / 6.0
t += dt
if i % nout == 0:
print('i: {0:4d}, t: {1:6.2f}, x: {2:9.6f}, y: {3:9.6f} , vx: {4:9.6f}, vy: {5:9.6f}'.format(i, t, r[0], r[1], v[0], v[1]))
gx.append(r[0])
gy.append(r[1])
im_line = ax.plot(gx, gy, 'b')
im_point = ax.plot(r[0], r[1], marker='.', color='b', markersize=10 )
im_time = ax.text(0.0, 0.1, 'time = {0:5.2f}'.format(t))
ims.append(im_line + im_point + [im_time])
# graph plot
ax.plot(0.0, 0.0, marker='.', color='r', markersize=10 )
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect('equal', 'datalim')
anm = animation.ArtistAnimation(fig, ims, interval=50)
anm.save('animation.gif', writer='pillow')
plt.show()前回作ったプログラムにグラフのアニメーション表示を追加してあります。
Pythonでアニメーション
今回はこのようなグラフを表示したいと思います。
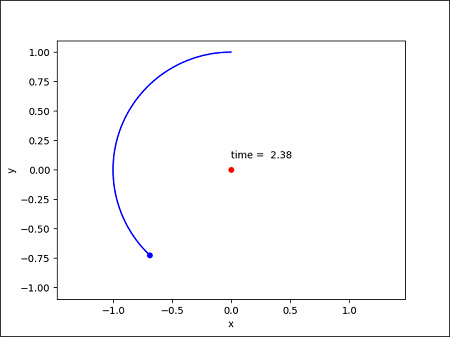
x-y平面の原点に太陽(赤い点)を表示し、地球を青い点、その軌跡を青い線で表示します。時間がわかるように太陽の上に時刻を表示させます。これをアニメーションの動画にしてみます。
では、プログラムを見ていきましょう。
import matplotlib.pyplot as plt
import matplotlib.animation as animation最初はいつもの matplotlib.pyplot のインポートです。2行目は、matplotlibのアニメーションモジュールをインポートしています。
# graph data array
gx = []
gy = []
ims = []
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)次は、グラフ表示で使う配列などの定義です。gx、gy はこれまでと同じように時間ごとの値を格納するための配列です。惑星の x座標とy座標を入れていきます。
ims はアニメーション用に各時刻のプロット図を格納するための配列です。動画の”コマ(フレーム)”を順番に入れていきます。
plt.figure() は新しく出てきた概念です。これまでグラフを描くときは、plt.plot() のようにしてプロットしていました。こういう書き方もあるのですが、matplotlib ではもう少し複雑な制御ができるように、オブジェクトを使った書き方があります。
fig = plt.figure() は、Figureというオブジェクトを fig という名前で定義しています。Figureというのはグラフの描画領域全体を表しています。
ax = fig.add_subplot(1, 1, 1) は、Axesというオブジェクトを ax という名前で定義しています。Axes は実際に描くグラフのことだと思ってください。add_subplot() は、以前複数のプロットを表示するときに subplot() を使いましたが、これと同じです。ここでは、1つのプロット図だけなので、(1, 1, 1) としています(1行×1列の1番目)。
つまり、Figure (fig) の中に、Axes (ax) が入っています。
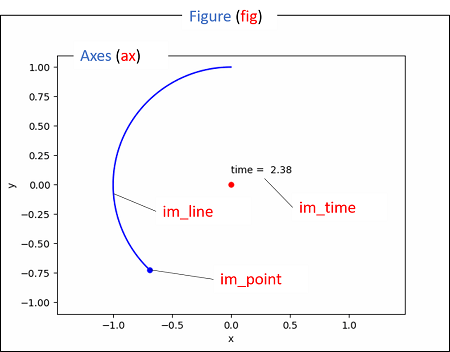
次に、実際にプロットする部分です。forループの中で各時刻のデータをプロットしていきます。
gx.append(r[0])
gy.append(r[1])
im_line = ax.plot(gx, gy, 'b')
im_point = ax.plot(r[0], r[1], marker='.', color='b', markersize=10 )
im_time = ax.text(0.0, 0.1, 'time = {0:5.2f}'.format(t))
ims.append(im_line + im_point + [im_time])gx.append(r[0]) は、惑星のx座標を gx に追加しています。惑星の座標は r というベクトルでした。これはx成分とy成分を持っていますが、ベクトル(配列)には最初の要素が0、次の要素が1という番号がついています。つまり、r[0] は r の最初の要素、すなわち x座標を意味しています。
gy.append(r[1]) は、同様に r の1番の要素であるy座標を gy に追加しています。
im_line = ax.plot(gx, gy, 'b') は、gx と gy をプロットしています。これは先程定義した、ax のグラフに対して行っています。'b' は、プロットの色を青色(blue)にするという意味です。gx、gy はこれまでと同様に、時々刻々のデータが入っていますので線で表示されます。そして、このプロットを im_line としています。
im_point = ax.plot(r[0], r[1], marker='.', color='b', markersize=10 ) は、現在時刻の惑星の位置 r をプロットしています。marker='.' は、表示を ・(点)にすると言う意味です。color='b' は先程と同様に青色にして、markersize=10 は表示する点の大きさを決めています。そして、このプロットは im_point という名前にしています。
im_time = ax.text(0.0, 0.1, 'time = {0:5.2f}'.format(t)) は、「time = ***」のように現在時刻をテキスト表示しています。表示する位置は、(0.0, 0.1) なので原点(太陽位置)の少し上です。format による出力は以前やりましたね。この表示は、im_time としています。
ims.append(im_line + im_point + [im_time]) は、前に作った ims の配列に、ここでプロットした im_line、im_point、im_time を合わせて格納しています。+してやると、同時に格納してくれます。im_timeだけ配列形式にしておいてください。これで各時刻ごとのコマを格納していきます。
# graph plot
ax.plot(0.0, 0.0, marker='.', color='r', markersize=10 )
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_aspect('equal', 'datalim')
anm = animation.ArtistAnimation(fig, ims, interval=50)
anm.save('animation.gif', writer='pillow')
plt.show()forループを抜けたところで、その他のグラフの調整とアニメーションの作成を行います。
ax.plot(0.0, 0.0, marker='.', color='r', markersize=10 ) は、原点に点を赤色(red)で表示しています。太陽のプロットです。
ax.set_xlabel('x')、ax.set_ylabel('y') は、x軸とy軸のラベル指定です。
ax.set_aspect('equal', 'datalim') は、グラフの縦横比を合わせています。通常だと横長のグラフになりますが、この命令を入れると縦横のスケールが1:1になるように揃います。なぜ縦横比を合わせるかというと、横長のグラフだと円が楕円のように表示されてしまって、軌道を見るのには不都合だからです。
anm = animation.ArtistAnimation(fig, ims, interval=50) は、アニメーションを作る部分です。fig は上で定義したFigureオブジェクトです。ims はforループの中で作った、各時刻のプロットが格納されている配列です。interval=50 は、各フレームの再生間隔を 50 ms にしています。
anm.save('animation.gif', writer='pillow') は、作ったアニメーションをファイルに保存しています。ファイル名は animation.gif です。これは、GIFアニメの形式で保存されます。(Pillowは画像処理用のライブラリでAnacondaに付属しています。)
plt.show() は、これまでも出てきたように、画面にプロットする命令です。
アニメーションの表示は、ちょっと難しいと感じるかもしれませんが、どこで何をやっているかわかるとそれほど複雑ではありません。何度か見直して理解してください。
if文による出力の制御
さて、あと一箇所説明だけ説明しておきます。forループの中に次の部分があります。
if i % nout == 0: これは初めて出てきましたが、if文というやつです。
if文は、if の後の条件が満たされたときだけ、その後の処理をするというものです。
今回は、時間刻みを小さくして計算精度を確保しておきたいのですが、そうすると全計算ステップ数が多くなってしまいます(nt = 10000ステップ)。アニメーションを作るときに、これだとコマ数が多くなりすぎます。そこで、何ステップかおきに出力させ、コマ数を間引きたいと思います。その制御をif文で行っています。
i はforループで増分されるステップ番号です。nout ごとに出力する場合は、i を nout で割って余りが0になるときに、出力させればよいです。i % nout は、i を nout で割った余りを計算しています。== 0 は、その余りが0であるかどうかを判定する部分です。
つまり、i % nout == 0 が満たされたときに、if文以下字下げしている部分が実行されます。ここでは、先程のアニメーション表示と、print文で画面に値を表示する部分が実行されます。このプログラムでは、nout = 20 としています。500コマのアニメーションが作成されるというわけです。
さて、これで惑星の軌道計算プログラムが完成しました。
長くなったので本日はこれで終わりにします。結果は次回見ていきましょう。
まとめ
Pythonで惑星の軌道計算プログラムを完成させました。アニメーションやif文など新しい処理が出てきましたが、これでプログラムの出来上がりです。
次回は、「科学技術計算講座2」の最終回です。計算結果を見ながら惑星がどのように運動しているか見ていきましょう。
